こんにちは。今回は徳島県の放物線の問題をやってみましょう。それではどうぞ。
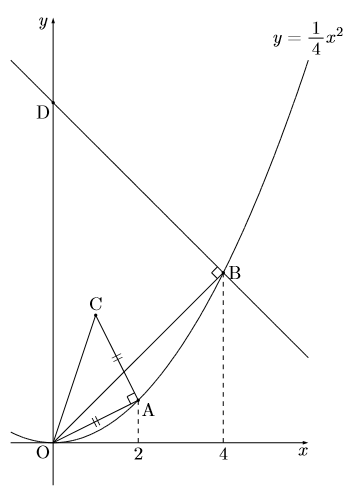
図のように, ![]() 座標がそれぞれ2, 4である2点A, Bを, 関数
座標がそれぞれ2, 4である2点A, Bを, 関数![]() のグラフ上にとり,
のグラフ上にとり, ![]() で, AO
で, AO![]() ACである直角三角形OACをつくる。また, 点Bを通り, 線分BOに垂直な直線が
ACである直角三角形OACをつくる。また, 点Bを通り, 線分BOに垂直な直線が![]() 軸と交わる点をDとする。(1)~(4)に答えなさい。
軸と交わる点をDとする。(1)~(4)に答えなさい。
(1) 点Bの![]() 座標を求めなさい。
座標を求めなさい。
(2) 直線BDの式を求めなさい。
(3) 点Aを通り,![]() 軸に平行な直線と線分OCとの交点をEとするとき, △OAEの面積を求めなさい。
軸に平行な直線と線分OCとの交点をEとするとき, △OAEの面積を求めなさい。
(4) ![]() 軸に平行な直線
軸に平行な直線![]() が△OACの面積を2等分するとき、
が△OACの面積を2等分するとき、![]() の値を求めなさい。
の値を求めなさい。
(H24徳島)
 数樂管理人のブログ
数樂管理人のブログ 


解答に書かれている直線OCの式、y=1/3xではなく、y=3xではないでしょうか?
ご指摘ありがとうございます。
修正しておきました。
また何かございましたらお願いします。