こんにちは。規則性の攻略方法です。等差数列に関してです。それではどうぞ。
規則性の攻略(差が一定の場合・等差数列)
〇規則性の問題は問題によるが差が一定かどうか, 4番目までは出てくる数字を調べたい。
〇大別して2パターン
【パターン1】 1番目, 2番目など図形が分けて書いてくれている場合は, 1番目, 2番目の図から規則を調べ3番目, 4番目の図を書いて, 数字を調べる。
【パターン2】 1番目, 2番目の図が書いてなく, 3番目, 4番目などのまとまった図形が書いてある場合は, パターン1とは逆に3番目, 4番目の図形から規則を調べ, 1番目, 2番目の図形を書いて, 数字を調べる。
〇調べた数字をもとに![]() 番目の式をつくる。
番目の式をつくる。
例 調べた数字が以下のような場合
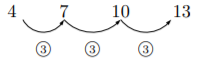
差が一定で3であるから, 高校生の等差数列の公式 : (初項)![]() (公差)
(公差)![]() を使いたいところですが, 要らない。
を使いたいところですが, 要らない。
次の考え方で中学生のは事足ります。上のはじめの数字が4, 差が3で一定の場合で![]() 番目を求める式は, 差が3なので3
番目を求める式は, 差が3なので3![]() とし, 3に何を足したらはじめの数字4になるかを考えると1なので,
とし, 3に何を足したらはじめの数字4になるかを考えると1なので, ![]() 番目の式は3
番目の式は3![]() 1となる。
1となる。
もう一つ例を上げてみます。
例 調べた数字が以下のような場合
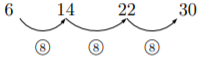
同じように考えてはじめの数字6, 差が8で一定で![]() 番目を求める式は, 差が8なので8
番目を求める式は, 差が8なので8![]() はじめの数字が6なので8に
はじめの数字が6なので8に![]() を足すとはじめの数字6になるので,
を足すとはじめの数字6になるので, ![]() 番目の式は
番目の式は![]() となる。
となる。
【別解】この考え方が難しいという方には, 1番目が6で, 2番目が14なので, これを座標と捉えて表すと, ![]() ,
, ![]() なので, この2点を通る直線の式を求めると,
なので, この2点を通る直線の式を求めると, ![]() となる。この式の右辺が
となる。この式の右辺が![]() 番目の式になっているので,
番目の式になっているので, ![]() としてもいいでしょう。隣り合う数字の差が一定の場合は一次関数として考えることができるので, これで答えは得られます。ただ, この解法は一次関数を習った生徒には伝わりますが, そうでない生徒には伝わらない話ではあります。
としてもいいでしょう。隣り合う数字の差が一定の場合は一次関数として考えることができるので, これで答えは得られます。ただ, この解法は一次関数を習った生徒には伝わりますが, そうでない生徒には伝わらない話ではあります。
〇入試問題を見ていこう(emathサイトから問題を拝借しました。)。鹿児島県の入試問題です。
1辺の長さが5cmである黒い正方形のタイルの周りを,1辺の長さが1cmである白い正方形のタイルで,すき間なく重ならないように囲む。たとえば,図1のように,黒いタイルが1枚のときは,白いタイルは全部で24枚必要であり,図2のように,黒いタイル2枚を横一列に並べるときは,白いタイルは全部で41枚必要である。このとき,次の(1), (2)の問いに答えよ。(鹿児島)
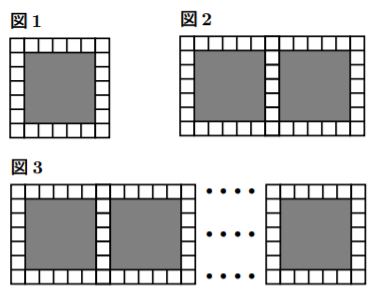
(1) 黒いタイル3枚を横一列に並べるとき,白いタイルは全部で何枚必要か。
(2) 図3のように,黒いタイル![]() 枚を横一列に並べるとき,白いタイルは全部で何枚必要か。
枚を横一列に並べるとき,白いタイルは全部で何枚必要か。![]() を用いて表せ。
を用いて表せ。
さて解いていくのだが, 1番目, 2番目の図が書いてくれてある。1番目は確かに24枚, 2番目は41枚, 3番目, 4番目の図を確認のために図を書くと, 以下のようになる。(注)数え上げのミスには気をつけよう。確認のためですので。
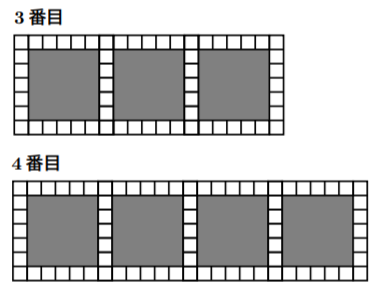
白のタイルを数えると3番目58枚, 4番目75枚。差を見てみると,
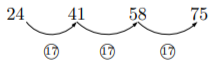
差が17で一定なので17![]() 。1番目の数字が24なので, 17に7を足すと24になる。
。1番目の数字が24なので, 17に7を足すと24になる。
よって, ![]() 番目は17
番目は17![]() 7(枚)
7(枚)
答(1)58枚,(2)17![]() 7(枚)
7(枚)
 数樂管理人のブログ
数樂管理人のブログ 

