こんにちは。相城です。今回は微分すると接線の傾きが求まることを書いておきます。
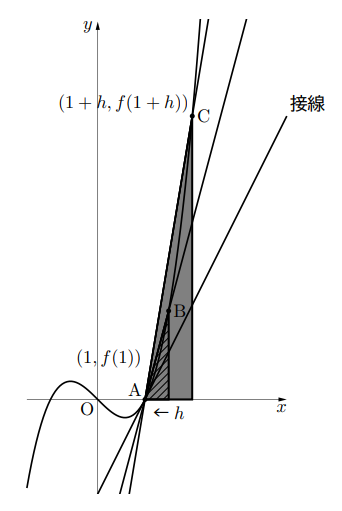
下の図は関数![]() のグラフである。微分したものがなぜ接線の傾きになるのか考えてみましょう。ここでは, グラフ上のA( 1, 0 )における接線の傾きを求めてみます。
のグラフである。微分したものがなぜ接線の傾きになるのか考えてみましょう。ここでは, グラフ上のA( 1, 0 )における接線の傾きを求めてみます。
まず点Aを通る直線を考えるとき, 直線AC, ABのように点Aとは異なる点を通る直線が考えられます。ここで点A以外のグラフ上の点をC![]() (∵
(∵![]() は点Aからの
は点Aからの![]() の増加量)とすると, 2点ACを通る直線の傾きは中学生の公式を使って, 次のように与えられます。
の増加量)とすると, 2点ACを通る直線の傾きは中学生の公式を使って, 次のように与えられます。
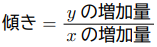
![]()
![]()
![]()
![]()
となります。
ここで, 接線とは接することであるから, この点Aからの増加量![]() は0に近くなり, 点Aではまさに0(厳密には0ではないが, 限りなく0である)になって, 接することになります。ですから
は0に近くなり, 点Aではまさに0(厳密には0ではないが, 限りなく0である)になって, 接することになります。ですから![]() で
で![]() となり, 接線の傾きは2になることが分かります。これが関数
となり, 接線の傾きは2になることが分かります。これが関数![]() の
の![]() における微分係数(接線の傾き)です。このように, グラフを細かく見ていくことができます。
における微分係数(接線の傾き)です。このように, グラフを細かく見ていくことができます。
一般に関数![]() の
の![]() における微分係数は次のように定義されます。
における微分係数は次のように定義されます。![]()
微分係数は![]() の値1つ1つに対応しますが, この1つ1つの対応を関数としてみたとき, 導関数(微分)は次のように定義されます。
の値1つ1つに対応しますが, この1つ1つの対応を関数としてみたとき, 導関数(微分)は次のように定義されます。![]()
実際, 上の![]() の微分を導関数の定義の
の微分を導関数の定義の![]() でやってみると,
でやってみると, ![]()
![]()
![]()
![]()
微分をご存知の方は, ![]() なら,
なら, ![]() となることは瞬時にお分かりだと思います。したがって,
となることは瞬時にお分かりだと思います。したがって, ![]() における微分係数(接線の傾き)は,
における微分係数(接線の傾き)は, ![]() となり, はじめに計算したものと一致します。このように, 導関数を求め(微分し), 接点の
となり, はじめに計算したものと一致します。このように, 導関数を求め(微分し), 接点の![]() 座標を代入することで接線の傾きが得られます。
座標を代入することで接線の傾きが得られます。
微分することで, 瞬間の変化の割合(傾き)が分かります。これによって, グラフを細かく見ていくことが可能です。また, 変化の割合が一定でないことは, そのグラフは曲線を描くことは言うまでもありません。
微分係数では![]() の値に応じて1つ1つ求めなければなりませんが, 今後微分係数の計算は導関数を求めて(微分して), それに必要な
の値に応じて1つ1つ求めなければなりませんが, 今後微分係数の計算は導関数を求めて(微分して), それに必要な![]() の値を代入することで, 所定の微分係数は得られるようになります。
の値を代入することで, 所定の微分係数は得られるようになります。
 数樂管理人のブログ
数樂管理人のブログ