こんにちは。相城です。
約数の基本問題を少し。定期テストに向けてご利用ください。
さて問題です。
(1) 20の正の約数をすべて求めよ。
(2) 36の約数をすべて求めよ。
(3) 72の正の約数の個数を求めよ。
(4) 400の正の約数の総和を求めよ。
(5) 12の倍数で正の約数の個数が10個である自然数を求めよ。

答え
(1) 1, 2, 4, 5, 10, 20
(2) ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, ±36
(3)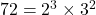
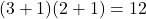 (個)
(個)
(4)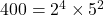 より正の約数の総和は
より正の約数の総和は
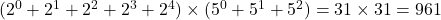
961
(5)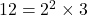
正の約数の個数が10個ということは
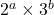 とすると
とすると 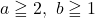 なので
なので
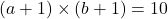 としたとき,
としたとき, 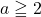 より
より
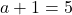 で
で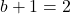 となること以外正の約数の個数が10個になることはないので,
となること以外正の約数の個数が10個になることはないので, 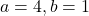
したがって、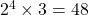
48
(2) ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, ±36
(3)
(4)
961
(5)
正の約数の個数が10個ということは
したがって、
48
 数樂管理人のブログ
数樂管理人のブログ 

