高校数学：整数：整数問題・余り①(合同式の考え方を用いて)

こんにちは。相城です。今回は合同式の問題ですが, 合同式は使わず答えを書いていきます。ただし, 考え方はよく似ていますので, 見ていきましょう。それでは問題です。

問題

(1) $21^{100}$ を5で割った余りを求めよ。
(2) $3^{200}$ を8で割った余りを求めよ。
(3) $4^{100}$ を13で割った余りを求めよ。
(4) $2^{300}$ を9で割った余りを求めよ。
(4) $33^{30}$ を90で割った余りを求めよ。(類愛媛大)

答え

(1) 21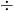 $\div$ 5の余りが1なので求める余りは 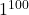$1^{100}$ を5で割った余りになる。よって1
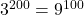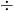(2) $3^{200}=9^{100}$ となる。9 $\div$ 8の余りが1なので求める余りは,
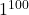$1^{100}$ を8で割った余りになる。よって1
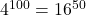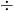(3) $4^{100}=16^{50}$ で, 16 $\div$ 13の余りは3となるので, 求める余りは, 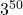$3^{50}$ を13で割った余りになる。
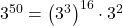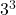$3^{50}=\left(3^3\right)^{16}\cdot3^2$ となる。 $3^3$ を13で割った余りは1だから, 求める余りは 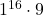$1^{16}\cdot9$ を13で割った余り。よって9
(4)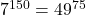 $7^{150}=49^{75}$ となる。49を15で割った余りは4なので, 求める余りは 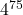$4^{75}$ を15で割った余りとなる。 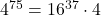$4^{75}=16^{37}\cdot4$ , 16を15で割った余りは1なので, 求める余りは 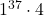$1^{37}\cdot4$ を15で割った余り。よって4
(5) $33^{30}=1089^{15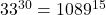}$ , 1089を90で割った余りは9なので, 求める余りは、 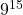$9^{15}$ を90で割った余り。 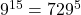$9^{15}=729^5$ なので, 729を90で割ると余りが9。したがって, 求める余りは 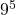$9^5$ を90で割った余りとなり, 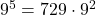$9^5=729\cdot9^2$ で、729を90で割った余りは9なので, 結局 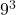$9^3$ を90で割ったのが求める余り。よって9

【GOM Mix】初心者でも簡単な動画編集ソフト

問題

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル