こんにちは。相城です。今回は2020年2月21日に行われた、東京都の問題からです。それではどうぞ。※一部Quicklatexで表現できない箇所は変更してます。ご了承ください。
下の図1に示した立体ABCD-EFGHは、AB![]() 6cm、AD
6cm、AD![]() 8cm、AE
8cm、AE![]() 12cmの直方体である。
12cmの直方体である。
頂点Cと頂点Fを結び、線分CF上にある点をPとする。
辺AB上にあり、頂点Bに一致しない点をQとする。
頂点Dと点P、頂点Dと点Q、点Pと点Qをそれぞれ結ぶ。
次の各問いに答えよ。
問1 次の( )の中の(a)(b)(c)に当てはまる数字をそれぞれ答えよ。点Pが頂点Fと、点Qが頂点Aとそれぞれ一致するとき、△DQPの面積は
(ab)![]() cm
cm![]() である。
である。
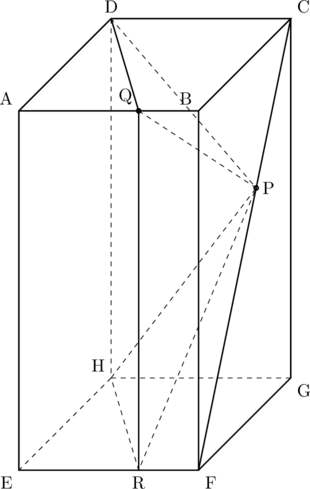
問2 次の( )の中の(d)(e)(f)に当てはまる数字をそれぞれ答えよ。
下の図2は、図1において、点Qを通り辺AEに平行な直線を引き、辺EFとの交点をRとし、頂点Hと点P、頂点Hと点R、点Pと点Rをそれぞれ結んだ場合を表している。
AQ![]() 4cm、CP : PF
4cm、CP : PF![]() 3 : 5のとき、立体P
3 : 5のとき、立体P![]() DQRHの体積は(def)cm
DQRHの体積は(def)cm![]() である。
である。
図1
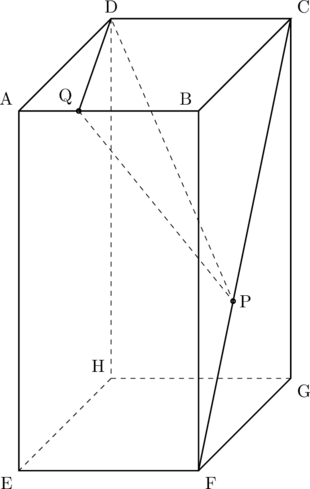
図2

答え
(1)
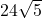 cm
cm
a、b、c 2、4、5
2、4、5
(2)
144cm
d、e、f 1、4、4
1、4、4
a、b、c
(2)
144cm
d、e、f
 数樂管理人のブログ
数樂管理人のブログ 

