こんにちは。相城です。さて、2020年2月21日に行われました、東京都の問題より平面図形の問題をどうぞ。選択問題がありましたが、選択肢は省いております。ご了承ください。
下の図1で、四角形ABCDは正方形である。
点Pは辺BC上にある点で、頂点B、頂点Cのいずれにも一致しない。
点Qは辺CD上にある点で、CP![]() CQである。
CQである。
頂点Aと点P、点Pと点Qをそれぞれ結ぶ。
次の各問いに答えよ。
問1 図1において、![]() とするとき、
とするとき、![]() の大きさを表す式を、書きなさい。
の大きさを表す式を、書きなさい。
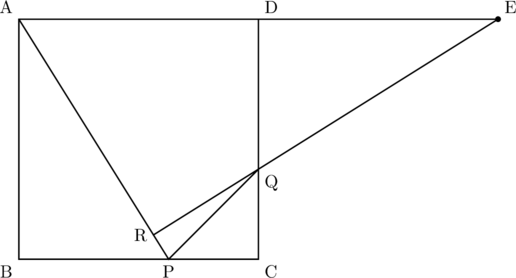
問2 下の図の図2は、図1において、辺ADをDの方向に延ばした延長線上にありAD![]() DEとなる点をE、点Eと点Qの方向に延ばした直線と線分APとの交点をRとした場合を表している。
DEとなる点をE、点Eと点Qの方向に延ばした直線と線分APとの交点をRとした場合を表している。
次の①、②に答えよ。
① △ABP≡△EDQであることを証明せよ。
② 次の( )の中の(あ)、(い)、(う)に当てはまる数字をそれぞれ答えよ。
図2において、AB![]() 4cm、BP
4cm、BP![]() 3cmのとき、線分EQの長さと線分QRの長さの比を最も簡単な整数の比で表すと、EQ : QR
3cmのとき、線分EQの長さと線分QRの長さの比を最も簡単な整数の比で表すと、EQ : QR![]() (あい) : (う)である。
(あい) : (う)である。
図1
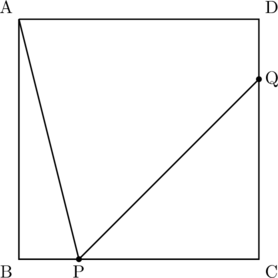
図2

答え
(1) 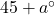
Pを通りABに平行な線を引きADとの交点をSとすると、
AB//PS//DCなので、平行線の錯角より
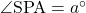 、
、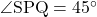
よって、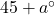
(2)
①
△ABPと△EDQで
仮定より
AD DE
DE BAより
BAより
BA DE・・・①
DE・・・①
CP CQとBC
CQとBC CDから
CDから
BP DQ・・・②
DQ・・・②
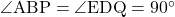 ・・・③
・・・③
①、②、③より
2組の辺とその間の角がそれぞれ等しいので
△ABP≡△EDQ
②
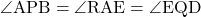
と が共通より、
が共通より、
△EDQ∽△ERA
三平方の定理より、EQ 5。またED
5。またED 4、EA
4、EA 8なので、
8なので、
5 : 6 4 : ER
4 : ER
ER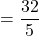 より、
より、
QR ER-EQ
ER-EQ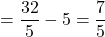
したがって
EQ : QR 5 :
5 : 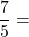 25 : 7
25 : 7
Pを通りABに平行な線を引きADとの交点をSとすると、
AB//PS//DCなので、平行線の錯角より
よって、
(2)
①
△ABPと△EDQで
仮定より
AD
BA
CP
BP
①、②、③より
2組の辺とその間の角がそれぞれ等しいので
△ABP≡△EDQ
②
と
△EDQ∽△ERA
三平方の定理より、EQ
5 : 6
ER
QR
したがって
EQ : QR
 数樂管理人のブログ
数樂管理人のブログ 

