TikZ：2020年度・神奈川県：平行四辺形と面積

2020年2月24日2022年5月29日

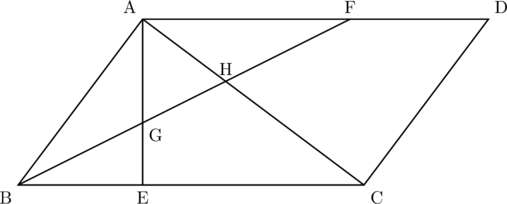
こんにちは。相城です。さて、2020年の2月に行われなした、神奈川県の入試問題より、平行四辺形と面積の問題です。それではどうぞ。

下の図のような平行四辺形ABCDがあり、辺BC上に点Eを辺BCと線分AEが垂直に交わるようにとり、辺AD上に点FをAB $=$ AFとなるようにとる。
また、線分BFと線分AEとの交点をG、線分BFと線分ACとの交点をHとする。
AB $=$ 15cm、AD $=$ 25cm、 $\angle{\\text{BAC}}=90^{\circ}$ のとき、三角形AGHの面積を求めなさい。

答え

$\dfrac{45}{2}$ cm $^2$
三平方の定理よりAC $=$ 20
△ABCの面積の関係より
$15\times20=25\times$ AEとなるので
AE $=$ 12。これを用いて△ABEで三平方の定理よりBE $=$ 9
また△AGF∽△EGBでAG : EG $=$ AF : EB $=$ 5 : 3・・・①
△AHF∽△CHBよりAH : CH $=$ AF : CB $=$ 3 : 5・・・②
①、②より△AGHは△AECの $\dfrac{5\times3}{8\times8}=\dfrac{15}{64}$ 倍。EC $=25-9=16$
よって、求める面積は
△AGH $=16\times12\times\dfrac{1}{2}\times\dfrac{15}{64}=\dfrac{45}{2}$
$\dfrac{45}{2}$ cm $^2$

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル