こんにちは。相城です。2020年群馬県の前期問題から平行四辺形と面積に関する問題です。それではどうぞ。
下の図の平行四辺形ABCDにおいて、点E、Fはそれぞれ辺AD、CD上の点であり、AC//EFである。次の(1)~(3)の問いに答えなさい。
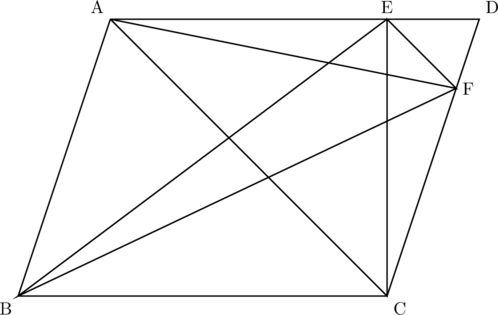
(1) 三角形ABCと三角形EBCの面積が等しいことを次のように証明した。
【ア】、【イ】に適する記号をそれぞれ入れなさい。
『証明』
△ABCと△EBCについて、ともに底辺をBCとして考えると、【ア】//【イ】より、高さが等しいといえる。したがって、底辺と高さがそれぞれ等しいので、△ABCと△EBCの面積は等しい。
(2) 三角形ADFと三角形CDEの面積が等しいことを証明しなさい。
(3) 平行四辺形ABCDの面積を96cm

答え
(1) 【ア】、【イ】AD、BC 順番はどちらでもよい(順不同) ADはAEでも大丈夫。
(2)
△ADFと△CDEで
△ADF=△AEF+△DEF・・・①
△CDE=△EFC+△DEF・・・②
△AEFと△EFCでEFを共通な底辺とすると
EF//ACであるから、高さも等しい。このことから、
底辺と高さがそれぞれ等しいので
△AEF=△EFC
よって①、②より
△ADFと△CDEの面積は等しい(△ADF=△CDE)
(3)
対角線BDを引いて, △BDFと△BDEの和として考える。
ここで, △BDF=△ADF=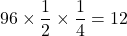
△BDE=△CDE=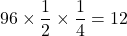
よって四角形EBFDの面積は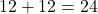 (cm
(cm )
)
別解
平行四辺形ABCDから△ABEと△BCFを取り除いた割合を
96cm にかけて求める。
にかけて求める。
平行四辺形ABCDの面積を96とすると、
△ABE=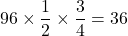
△BCF=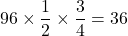
よって
四角形EBFD=平行四辺形ABCD-△ABE-△BCFであるから
四角形EBFD=96-36-36=24
24cm
別解 平行四辺形の面積の割合を1とする。
△ABEの割合が全体の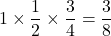
△BCFの割合が全体のの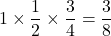 であるから、四角形EBFDの割合は
であるから、四角形EBFDの割合は
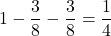
よって四角形EBFDの面積は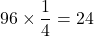 cm
cm
*)平行四辺形の面積の割合を1とせず面積をSとしてもよい。
(2)
△ADFと△CDEで
△ADF=△AEF+△DEF・・・①
△CDE=△EFC+△DEF・・・②
△AEFと△EFCでEFを共通な底辺とすると
EF//ACであるから、高さも等しい。このことから、
底辺と高さがそれぞれ等しいので
△AEF=△EFC
よって①、②より
△ADFと△CDEの面積は等しい(△ADF=△CDE)
(3)
対角線BDを引いて, △BDFと△BDEの和として考える。
ここで, △BDF=△ADF=
△BDE=△CDE=
よって四角形EBFDの面積は
別解
平行四辺形ABCDから△ABEと△BCFを取り除いた割合を
96cm
平行四辺形ABCDの面積を96とすると、
△ABE=
△BCF=
よって
四角形EBFD=平行四辺形ABCD-△ABE-△BCFであるから
四角形EBFD=96-36-36=24
24cm
別解 平行四辺形の面積の割合を1とする。
△ABEの割合が全体の
△BCFの割合が全体のの
よって四角形EBFDの面積は
*)平行四辺形の面積の割合を1とせず面積をSとしてもよい。
 数樂管理人のブログ
数樂管理人のブログ 


遅いかもしれないんですが、点Bと点Dを結んで△BEDとBDFに分けて等積変形するのも面白いかもしれません。
その方が早いですね。
AE:EDの比の意味が分かりました。
△BDE=△CDE、△BDF=△ADFですからね。
アドバイスありがとうございます。