こんにちは。相城です。円錐に関するあれこれをまとめました。用途などを知りたい方は, 攻略法の円錐をご覧ください。下部にリンク張っておきます。
円錐の見取り図と展開図を示しておきます。
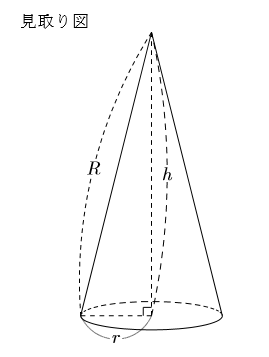
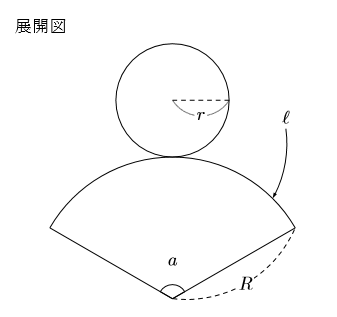
円錐の公式
体積![]()
![]()
側面積
![]()
または,
![]()
②の方が登場率は高い。
表面積
![]()
または,
![]()
登場率は④の方が高い。
側面の扇形の中心角
![]()
公式の証明などは以下の記事をご覧ください。
 中学数学:円錐関連の公式の導出
中学数学:円錐関連の公式の導出こんにちは。相城です。円錐に関するあれこれをまとめました。用途などを知りたい方は, 攻略法の円錐をご覧ください。下部にリンク張っておきます。
円錐の見取り図と展開図を示しておきます。


円錐の公式
体積![]()
![]()
![]()
![]()
![]()
![]()
![]()
公式の証明などは以下の記事をご覧ください。
 中学数学:円錐関連の公式の導出
中学数学:円錐関連の公式の導出