こんにちは。相城です。今回は三角錐を2つに分けたときの頂点を含む部分と,もとの三角錐との体積比の公式の紹介と証明を行ってみたいと思います。
下の図の三角錐で, 三角錐![]() と三角錐
と三角錐![]() の体積比は
の体積比は![]() になる。
になる。
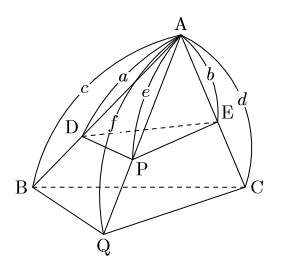
このことは, 三角錐![]() の体積は三角錐
の体積は三角錐![]() の体積の
の体積の![]() 倍であることを意味し, さらに細かく言えば, 三角錐
倍であることを意味し, さらに細かく言えば, 三角錐![]() の体積は三角錐
の体積は三角錐![]() の体積の
の体積の![]() 倍
倍
になることを意味している。
証明
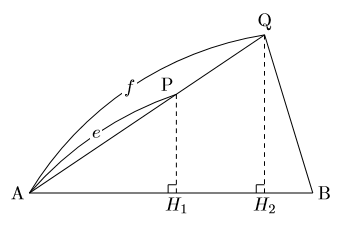
△ABCを底面として三角錐を考えると, 公式より底面の面積比は![]() である。 ここでその底面に対する高さは, 上の図から, △AH
である。 ここでその底面に対する高さは, 上の図から, △AH![]() P∽△AH
P∽△AH![]() Qを使って,
Qを使って,
![]()
よって,
三角錐
△ABCを底面とし, △ABCの面積を![]() とすると, △ADEの面積は
とすると, △ADEの面積は![]() である。それぞれの底面に対する三角錐の高さのは, 図よりPH
である。それぞれの底面に対する三角錐の高さのは, 図よりPH![]() ,QH
,QH![]() であるから,
であるから,
三角錐![]()
三角錐![]()
である。
三角錐![]() 三角錐
三角錐![]()
ここでPH![]() : QH
: QH![]()
よってPH![]() , QH
, QH![]() (
(![]() は0でない定数)とおけるので, これを①に代入すると,
は0でない定数)とおけるので, これを①に代入すると,
三角錐![]() 三角錐
三角錐![]()
この比にの両方に![]() をかけて,
をかけて, ![]() で割ると,
で割ると,
三角錐![]() 三角錐
三角錐![]()
となる。
 数樂管理人のブログ
数樂管理人のブログ 

