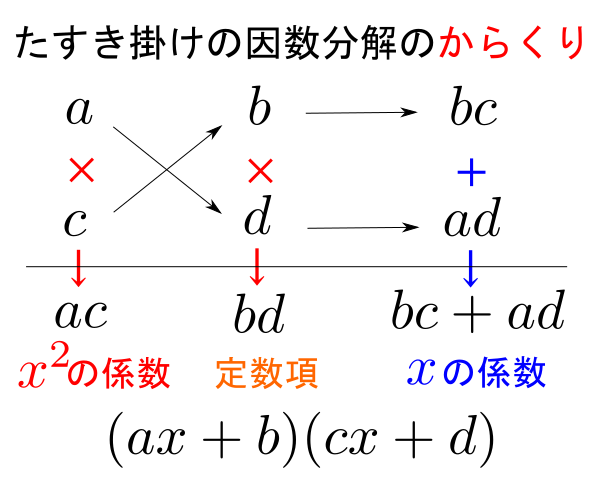
高校数学の代名詞?の1つ, たすき掛けの因数分解を書いておきます。
次の展開公式の逆ですね。以下の乗法公式![]()
の逆, つまり, ![]()
の因数分解のことです。この因数分解は以下のからくりを用いて完成させます。![]() の係数を構成する2数
の係数を構成する2数![]() を縦に書き, 定数項を構成する2数
を縦に書き, 定数項を構成する2数![]() を縦に書き, たすきのようにバッテン(×)に掛け算して和を求めると
を縦に書き, たすきのようにバッテン(×)に掛け算して和を求めると![]() の係数になるように
の係数になるように![]() を配置する。これができると,
を配置する。これができると, ![]() と
と![]() というように横に見て
というように横に見て![]() と因数分解できるわけです。
と因数分解できるわけです。
実際の問題をやりながら体得していきましょう。
例題
【例題】![]() を因数分解しなさい。
を因数分解しなさい。
公式①より, 問題中の式の![]() の係数3と定数項の5は単純に2数の積で決まります。積が3になる2数は, 1と3か
の係数3と定数項の5は単純に2数の積で決まります。積が3になる2数は, 1と3か![]() と
と![]() ですが, 先頭の符号は基本的に
ですが, 先頭の符号は基本的に![]() の符号で, 後ろの数(この場合5)で符号の調整は行います。よって, 上の
の符号で, 後ろの数(この場合5)で符号の調整は行います。よって, 上の![]() ,
, ![]() に当たるものが, 1と3になります。次に定数項は5なので, 積が5になる組合せは, 先と同様, 1と5か
に当たるものが, 1と3になります。次に定数項は5なので, 積が5になる組合せは, 先と同様, 1と5か![]() と
と![]() ですが,
ですが, ![]() の係数が正の数なので, 両方負の数ということはあり得ない(
の係数が正の数なので, 両方負の数ということはあり得ない(![]() の係数が負になるから)ことになります。したがって, 積が5になる組は1と5になります。これを前途した, たすき掛けに配置し, たすき掛けした結果和をとると,
の係数が負になるから)ことになります。したがって, 積が5になる組は1と5になります。これを前途した, たすき掛けに配置し, たすき掛けした結果和をとると, ![]() の係数16になればいい。つまり, この配置の仕方は以下になります。
の係数16になればいい。つまり, この配置の仕方は以下になります。
よって, 例題の答えは![]() となります。
となります。
もう少し例題をしてみましょう。
【例題】![]() を因数分解しなさい。
を因数分解しなさい。
以下, 与式を![]() についての2次式とみて,
についての2次式とみて, ![]() は定数項として話を進めます。
は定数項として話を進めます。
まず, ![]() は正の数なので, 6になる組は(2, 3)か(1, 6)になります。次に
は正の数なので, 6になる組は(2, 3)か(1, 6)になります。次に![]() (以下話が見えやすいよう
(以下話が見えやすいよう![]() を略してます。)になる組を考えるのですが, このとき,
を略してます。)になる組を考えるのですが, このとき, ![]() ではなく,
ではなく, ![]() の絶対値の14になる組を考えて, 足したり引いたりして,
の絶対値の14になる組を考えて, 足したり引いたりして, ![]() の係数5になる組を探るのです。ですから積が14になる組は(2, 7)か(1, 14)になり,
の係数5になる組を探るのです。ですから積が14になる組は(2, 7)か(1, 14)になり, ![]() が(2, 3)で,
が(2, 3)で, ![]() が(2, 7), (1, 14)で掛け算の組み合わせを試行すると,
が(2, 7), (1, 14)で掛け算の組み合わせを試行すると, ![]() ,
, ![]() ,
, ![]() ,
, ![]() でどの結果も差が5になる組はありません。したがって,
でどの結果も差が5になる組はありません。したがって, ![]() が2と3ではないことになります。
が2と3ではないことになります。![]() を(1, 6)として, 積が14になる組(2, 7), (1, 14)で試行すると, (1, 6), (1, 14)の積の組み合わせでは5がつくれないことは分かってくるでしょう。また(1, 6), (2, 7)の積の組でも6と7をかける組み合わせは考えなくてもいいでしょう。そうやって消去していくと残る積の組合せは,
を(1, 6)として, 積が14になる組(2, 7), (1, 14)で試行すると, (1, 6), (1, 14)の積の組み合わせでは5がつくれないことは分かってくるでしょう。また(1, 6), (2, 7)の積の組でも6と7をかける組み合わせは考えなくてもいいでしょう。そうやって消去していくと残る積の組合せは, ![]() となり,
となり, ![]() で
で![]() の係数5ができました。このときはじめて, 7にマイナスをつければいいことが分かるので,
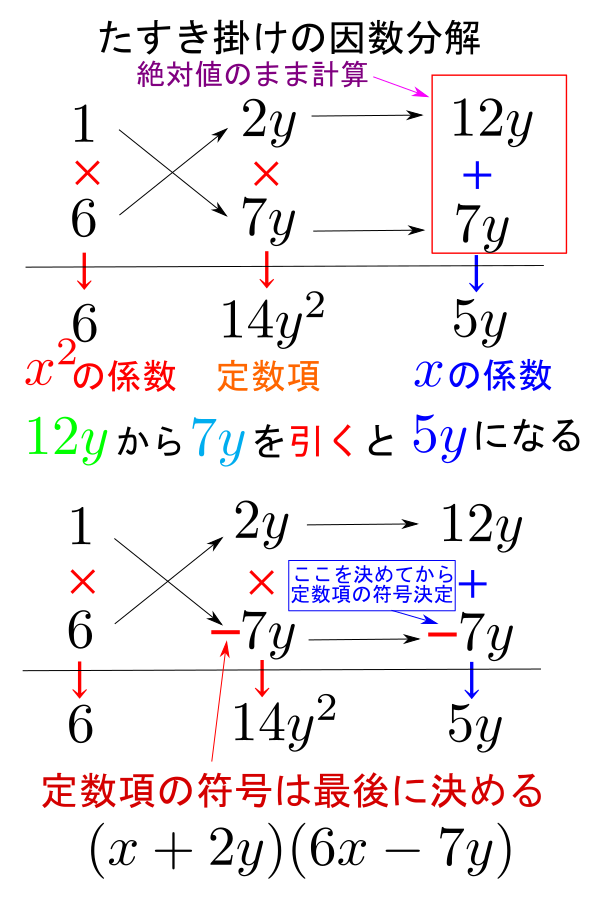
の係数5ができました。このときはじめて, 7にマイナスをつければいいことが分かるので, ![]() となります。このように, たすき掛けの因数分解を行うときは絶対値のまま考えて, 最後に符号で調整していくと,うまくいくことが多いです。以下の画像でその様子を触れておきます。
となります。このように, たすき掛けの因数分解を行うときは絶対値のまま考えて, 最後に符号で調整していくと,うまくいくことが多いです。以下の画像でその様子を触れておきます。
よって, 答えは![]() となります。
となります。
このようなものがたすき掛けを用いた因数分解です。慣れてくると見えてきますので, トライアンドエラーをくり返しながら因数分解に挑戦してみてください。
もっとコツ(時間短縮)を知りたい方は以下の記事を参照ください。
 高校数学:式と計算:たすき掛けの因数分解のコツ
高校数学:式と計算:たすき掛けの因数分解のコツ 数樂管理人のブログ
数樂管理人のブログ