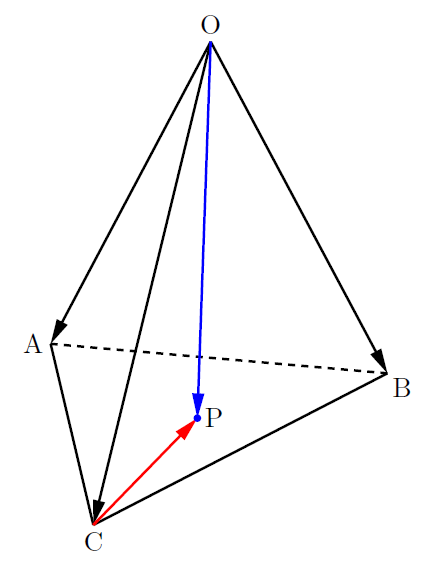
こんにちは。相城です。今回は空間ベクトルの必須アイテムである公式についてです。以下のようなものです。
四面体![]() において,
において, ![]() が△
が△![]() (平面
(平面![]() )上にあるとき,
)上にあるとき, ![]() で,
で, ![]() となることを証明したいと思います。
となることを証明したいと思います。
![]() ,
, ![]() ,
, ![]() とおくと,
とおくと, ![]()
Pは△![]() (平面
(平面![]() )上にあるので,
)上にあるので, ![]() と置け,
と置け, ![]() ,
, ![]() であるから,
であるから, ![]() は次のようになる。
は次のようになる。![]()
これを![]() に代入すると,
に代入すると,![]()
展開して, 整理すると, ![]()
![]() と置くと,
と置くと, ![]()
となり, このとき, ![]() である。
である。
ちなみに点![]() が△
が△![]() の内部(周上を含む)にあるときは,
の内部(周上を含む)にあるときは, ![]() である。
である。
また, ![]() ならば点
ならば点![]() は平面
は平面![]() 上にあり, 点
上にあり, 点![]() が平面
が平面![]() 上にあるならば,
上にあるならば, ![]() という, 必要十分条件の関係にあることも押さえておきましょう。
という, 必要十分条件の関係にあることも押さえておきましょう。
 数樂管理人のブログ
数樂管理人のブログ