こんにちは。平面ベクトルで, 分点の公式とかやってると, 点Pは直線AB上にあるので, 係数の和は1になるみたいなことが登場するのですが, それを書いておきます。内分点, 外分点の話は別に書くとして, 書いていきます。
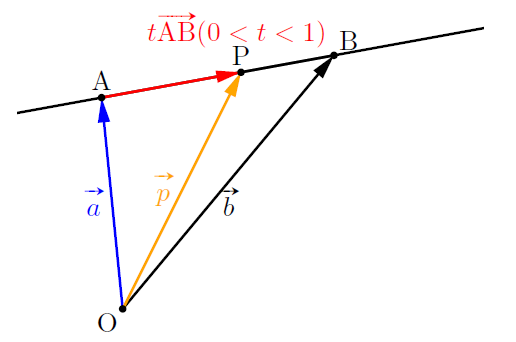
Pが直線AB上にあるとき, ![]() 図のようになります。
図のようになります。
![]()
![]()
![]()
![]() とすれば,
とすれば, ![]()
このとき, ![]() で,
で, ![]() より,
より, ![]() である。
である。
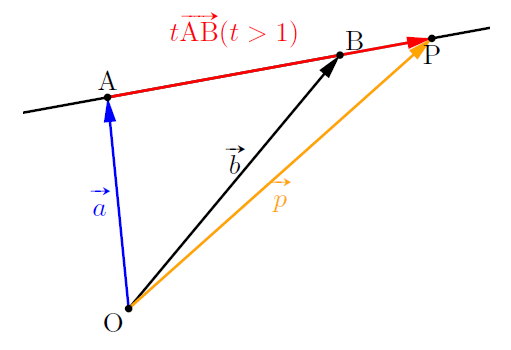
PがABのBの側の外側にあるとき, ![]() のとき,
のとき,
内分点と同様の考え方から, ![]()
![]()
![]()
![]() とすれば,
とすれば,![]()
このとき, ![]() で,
で, ![]() より,
より, ![]()
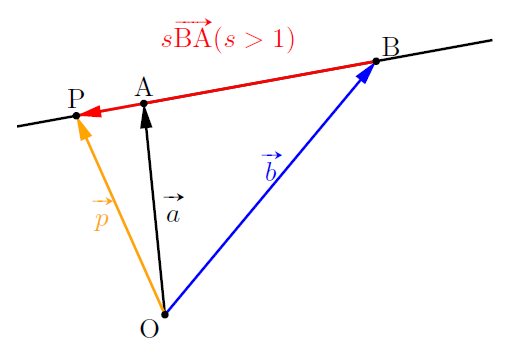
PがABのAの側の外側にあるとき, ![]() のとき,
のとき,
![]()
![]()
![]()
![]() とすれば,
とすれば,![]()
このとき, ![]() で,
で, ![]() より,
より, ![]()
以上より, ![]() において, 点Pが直線AB上にあるなら,
において, 点Pが直線AB上にあるなら, ![]() が成り立つ。その逆も成り立つ。
が成り立つ。その逆も成り立つ。
 数樂管理人のブログ
数樂管理人のブログ