こんにちは。今回は円の接線の公式について触れておきます。基本的な証明かどうかは分かりませんが, 証明を載せておきます。
円の接線の公式
円の接線の公式(接点が与えられている)
(A)円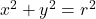 上の点
上の点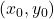 における接線の方程式
における接線の方程式
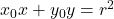
(B)円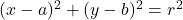 上の点
上の点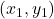 における接線の方程式
における接線の方程式
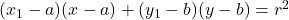
(B)円
(A)の証明
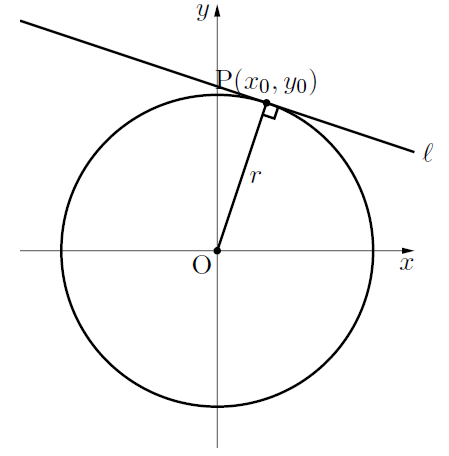
円の式を![]() とし, 接点をP
とし, 接点をP![]() とすると, 直線OPの傾きは
とすると, 直線OPの傾きは![]() であるから,
であるから,
接線の方程式![]() の傾き
の傾き![]() は,
は, ![]() なので,
なので, ![]() ,
,
傾き![]() で点
で点![]() を通るので,
を通るので, ![]() の式は
の式は![]()
両辺![]() かけて整理すると,
かけて整理すると, ![]()
となりますが, P![]() は円
は円![]() 上の点なので,
上の点なので, ![]() が成り立ちます。
が成り立ちます。
したがって, ![]() は
は![]()
となり, 公式を得ます。
使い方の例
【例題】円![]() 上の点(4, 3)における接線の方程式を求めよ。
上の点(4, 3)における接線の方程式を求めよ。
【解答】![]() (答)
(答)
続いて(B)の証明
中心が![]() 半径が
半径が![]() の円, 接点がP
の円, 接点がP![]() の場合,
の場合,
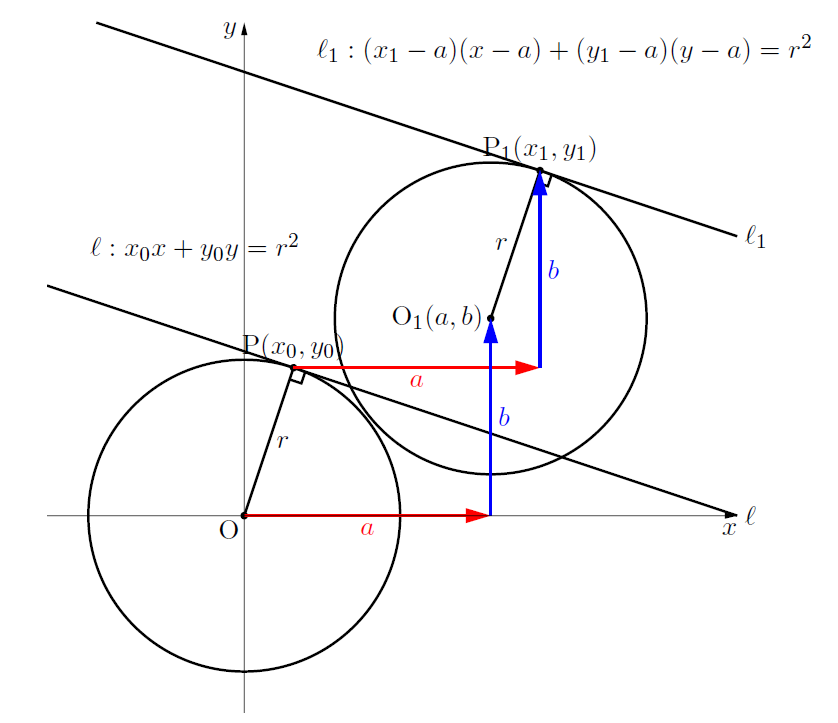
証明するのに, 先ほど証明した接線の方程式![]() を平行移動して考えます。
を平行移動して考えます。
つまり,
中心O![]() O
O![]() ,
,
接点P![]() P
P![]()
に移動します。
このとき円の中心が原点で半径が![]() , 接点P
, 接点P![]() における接線の方程式
における接線の方程式![]() も
も![]() 軸方向に
軸方向に![]() ,
, ![]() 軸方向に
軸方向に![]() 平行移動しているので,
平行移動しているので, ![]() をそのように平行移動させると,
をそのように平行移動させると, ![]()
このとき, 各点も![]() 軸方向に
軸方向に![]() ,
, ![]() 軸方向に
軸方向に![]() 平行移動しているので,
平行移動しているので, ![]() と
と![]() の間には次のような関係式が成り立ちます。
の間には次のような関係式が成り立ちます。![]()
![]()
これから, ![]()
![]()
これらを![]() に代入し,
に代入し, ![]()
を得る。
使い方の例
【例題】円![]() 上の点
上の点![]() における接線の方程式を求めよ。
における接線の方程式を求めよ。
【解答】![]()
![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 

