2次方程式と3次方程式の解と係数の関係

こんにちは。今回は2次方程式と3次方程式の解と係数の関係について書いていきます。単に公式の導出ですので、そんなの知ってるよって方は得るものは少ないかもです。それではどうぞ。

2次方程式の解と係数の関係について

2次方程式の解と係数の関係

2次方程式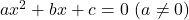 $ax^2+bx+c=0\ (a\neq0)$ の2つの解を 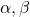$\alpha, \beta$ とすると,
$\alpha+\beta=-\dfrac{b}{a}$
$\alpha\beta=\dfrac{c}{a}$
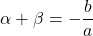
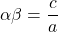
が成り立つというもの

【導出】
2次方程式を $ax^2+bx+c=0\ (a\neq0)\cdots\textcircled{\scriptsize 1}$ とし, $\textcircled{\scriptsize 1}$ の両辺を $a$ で割って, $x^2$ の係数を1にしておきます。
つまり, 先の2次方程式を
$x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0\cdots\textcircled{\scriptsize 2}$ とする。
この方程式の2つの解を $\alpha, \beta$ とすると, $\textcircled{\scriptsize 2}$ は, 次のように因数分解できる
$(x-\alpha)(x-\beta)=0$
これを展開すると
$x^2-(\alpha+\beta)x+\alpha\beta=0\cdots\textcircled{\scriptsize 3}$
$\textcircled{\scriptsize 2}$ と $\textcircled{\scriptsize 3}$ の係数を比較すると,
$-(\alpha+\beta)=\dfrac{b}{a}$
$\alpha\beta=\dfrac{c}{a}$
となり, 初めの関係式
$\alpha+\beta=-\dfrac{b}{a}$
$\alpha\beta=\dfrac{c}{a}$
が得られる。

3次方程式の解と係数の関係について

3次方程式の解と係数の関係

3次方程式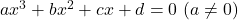 $ax^3+bx^2+cx+d=0\ (a\neq0)$ の2つの解を 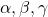$\alpha, \beta, \gamma$ とすると,
$\alpha+\beta+\gamma=-\dfrac{b}{a}$
$\alpha\beta+\beta\gamma+\gamma\alpha=\dfrac{c}{a}$
$\alpha\beta\gamma=-\dfrac{d}{a}$
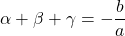
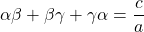
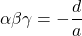
が成り立つというもの

【導出】
3次方程式を $ax^3+bx^2+cx+d=0\ (a\neq0)\cdots\textcircled{\scriptsize 1}$ とし, $\textcircled{\scriptsize 1}$ の両辺を $a$ で割って, $x^3$ の係数を1にしておきます。
つまり, 先の3次方程式を
$x^3+\dfrac{b}{a}x^2+\dfrac{c}{a}x+\dfrac{d}{a}=0\cdots\textcircled{\scriptsize 2}$ とする。
この方程式の3つの解を $\alpha, \beta, \gamma$ とすると, $\textcircled{\scriptsize 2}$ は, 次のように因数分解できる
$(x-\alpha)(x-\beta)(x-\gamma)=0$
これを展開すると
$x^3-(\alpha+\beta+\gamma)x^2+(\alpha\beta+\beta\gamma+\gamma\alpha)x-\alpha\beta\gamma=0\cdots\textcircled{\scriptsize 3}$
$\textcircled{\scriptsize 2}$ と $\textcircled{\scriptsize 3}$ の係数を比較すると,
$-(\alpha+\beta+\gamma)=\dfrac{b}{a}$
$\alpha\beta+\beta\gamma+\gamma\alpha=\dfrac{c}{a}$
$-\alpha\beta\gamma=\dfrac{d}{a}$
となり, 初めの関係式
$\alpha+\beta+\gamma=-\dfrac{b}{a}$
$\alpha\beta+\beta\gamma+\gamma\alpha=\dfrac{c}{a}$
$\alpha\beta\gamma=-\dfrac{d}{a}$
が得られる。