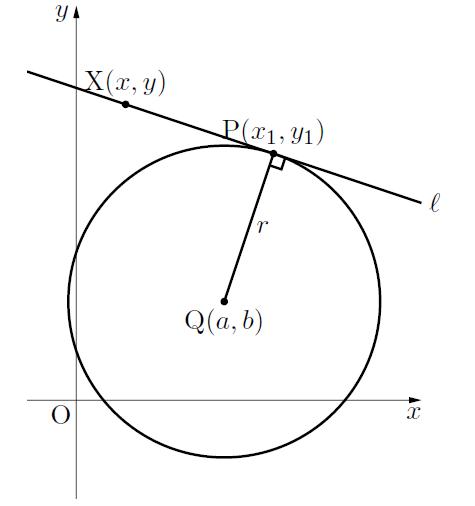こんにちは。今回は円の接線をベクトルを用いて証明しておこうと思います。
円の接線の公式(接点が与えられている)
(A) 円![]() 上の点
上の点![]() における接線の方程式
における接線の方程式![]()
(B) 円![]() 上の点
上の点![]() における接線の方程式
における接線の方程式![]()
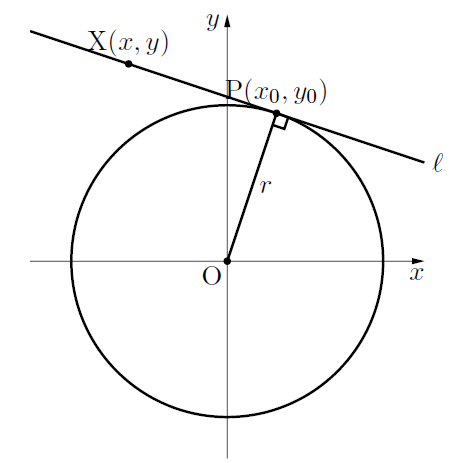
(A)の証明
円の方程式を![]() とし, 接点をP
とし, 接点をP![]() , 円の中心(原点)をOとし, 接線
, 円の中心(原点)をOとし, 接線![]() 上の点をX
上の点をX![]() とする。
とする。
このとき, ![]()
![]()
で, ![]() なので, 内積が0になる。
なので, 内積が0になる。
これを利用すると, ![]()
![]()
![]()
また, ![]() である。
である。
よって, ![]()
(B)の証明
円の方程式を![]() とし, 接点P
とし, 接点P![]() , 円の中心をQとし, 接線
, 円の中心をQとし, 接線![]() 上の点をX
上の点をX![]() とする。
とする。
このとき,![]()
![]()
で, ![]() なので, 内積が0になる。
なので, 内積が0になる。
これを利用すると,![]()
![]()
また, P![]() は円上の点なので,
は円上の点なので, ![]()
![]() から,
から, ![]()
![]()
よって,![]()
 数樂管理人のブログ
数樂管理人のブログ