emath：高校数学：円の接線(円の外部から)の攻略

【GOM Mix】初心者でも簡単な動画編集ソフト

こんにちは。今回は円の接線で円の外部の点から円に接線を引く場合を考えてみましょう。円の外部の点からは2本の接線が引けるのですが, 答えが1つしか出ないこともあります。今回はそれには触れていません。別記事で触れることにします。今回は素直に2本の接線が求まる場合を取り上げています。それではどうぞ。

例題を見ていこう

【例題】点(3, 1)から円 $(x-1)^2+(y+5)^2=10$ に引いた接線の方程式を求めなさい。

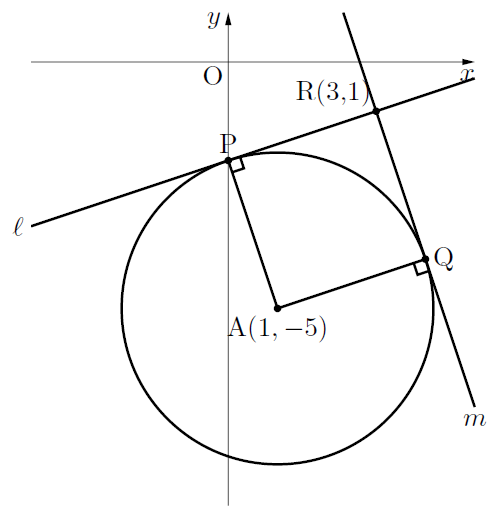
イメージとしてはこのような図になります。解法は主に3通りあります。

①直線と距離の関係から解く

結構頻度が高いと思います。比較的計算も楽です。それではいってみましょう。
2本の接線は $x$ 軸に垂直ではないので,
求める直線を $y=m(x-3)-1$ とおく。このとき, $mx-y-3m-1=0$ であり, この直線と円の中心 $(1,-5)$ との距離を求めると,
$\dfrac{\left|m+5-3m-1\right|}{\sqrt{m^2+1}}=\dfrac{\left|-2m+4\right|}{\sqrt{m^2+1}}$
この距離が, 円の半径 $\sqrt{10}$ と一致すれば接することになるので,
$\dfrac{\left|-2m+4\right|}{\sqrt{m^2+1}}=\sqrt{10}$
$\left|-2m+4\right|=\sqrt{10}\sqrt{m^2+1}$
両辺2乗して,
$(-2m+4)^2=10(m^2+1)$
$6m^2+16m-6=0$
$3m^2+8m-3=0$
$(m+3)(3m-1)=0$
$m=\dfrac13, -3$
$m=\dfrac13$ のとき,
$y=\dfrac13 x-2$
$m=-3$ のとき,
$y=-3x+8$
よって求める接線の方程式は, $y=\dfrac13 x-2$ , $y=-3x+8$

②接線の公式を利用して解く

円の接点をP $(x_0, y_0)$ とおくと, 円の接線の方程式は,
$(x_0-1)(x-1)+(y_0+5)(y+5)=10$
これが, $(3, -1)$ を通るので, 代入すると,
$2(x_0-1)+4(y_0+5)=10$
両辺2で割って, 整理すると,
$x_0+2y_0+4=0\cdots\textcircled{\scriptsize 1}$
また, P $(x_0, y_0)$ は円周上の点なので,
$(x_0-1)^2+(y_0+5)^2=10\cdots\textcircled{\scriptsize 2}$ が成り立つ。
$\textcircled{\scriptsize 1}$ から, $x_0=-2y_0-4$ として, $\textcircled{\scriptsize 2}$ に代入すると,
$(-2y_0-5)^2+(y_0+5)^2=10$
$5y_0^2+30y_0+40=0$
両辺5で割って,
$y_0^2+6y_0+8=0$
$(y_0+2)(y_0+4)=0,\ y_0=-2,-4$
$y_0=-2$ のとき, $x_0=0$ つまり, 接点が $(0,-2)$
$y_0=-4$ のとき, $x_0=4$ つまり, 接点が $(4, -4)$
接点が $(0,-2)$ のとき,
$-(x-1)+3(y+5)=10$ より, $-x+3y+6=0$
接点が $(4, -4)$ のとき,
$3(x-1)+y+5=10$ より, $3x+y-8=0$
よって, 求める接線は, $-x+3y+6=0$ , $3x+y-8=0$
接点を求めるときかは求めちゃうので, 便利かなと思います。

③代入して判別式＝0

計算量が比較的多い解法になります。あまりお勧めはしません。
2本の接線は $x$ 軸に垂直ではないので,
求める接線の方程式を $y=m(x-3)-1$ と置いて, 円の方程式に代入すると,
$(x-1)^2+\left\{m(x-3)+4\light\}^2=10$
$x^2-2x+1+m^2x^2-6m^2x+9m^2+8mx-24m+6=0$
$(1+m^2)x^2+(-6m^2+8m-2)x+9m^2-24m+7=0$
$(1+m^2)x^2-2(3m^2-4m+1)x+9m^2-24m+7=0$
これに $D/4=0$ を用いると,
$(3m^2-4m+1)^2-(1+m^2)(9m^2-24m+7)=0$
これを展開して計算すると,
$6m^2+16m-6=0$
$3m^2+8m-3=0$
$(m+3)(3m-1)=0$
$m=\dfrac13, -3$
$m=\dfrac13$ のとき,
$y=\dfrac13 x-2$
$m=-3$ のとき,
$y=-3x+8$
よって求める接線の方程式は, $y=\dfrac13 x-2$ , $y=-3x+8$

【GOM Mix】初心者でも簡単な動画編集ソフト

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル