emath：高校数学：円の接線(円の外部から2)

こんにちは。今回は円の外部からの接線を求めるときに, $x$ 軸に垂直になる方程式を含む場合について書いておきます。書いておくだけで, 特に技があるわけではないので, 補足程度と思ってください。

例題を見ていこう

点(3,5)から円 $x^2+y^2=9$ に引いた接線の方程式を求めよ。

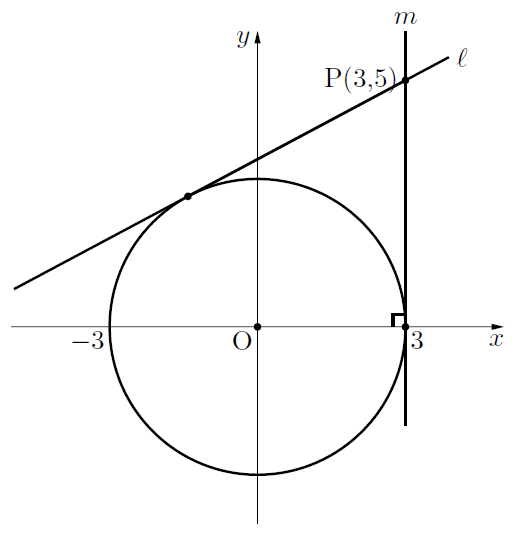
結論から言うと, この場合, この記事で書いた解法のうち, 傾きを $m$ と置いた解法では, $m$ の値は1つしか求まらないんですね。なぜかと言うと, $y=m(x-a)+b$ という式の表し方では, $x=k$ ( $k$ は実数)という式が表せないんです。実際それを書いておきます。

円の中心と直線との距離が半径と一致

解法①　直線と円の中心の距離が半径に一致
求める直線を $y=m(x-3)+5$ と置くと, $mx-y-3m+5=0$ となり,
円の中心(原点)からの距離が半径3に一致すると置くと,
$\dfrac{\left|-3m+5\right|}{\sqrt{m^2+1}}=3$
$\left|-3x+5\right|=3\sqrt{m^2+1}$
両辺2乗して整理すると,
$30m=16$
$m=\dfrac{8}{15}$
このとき, 求める求める接線の1つは, $y=\dfrac{8}{15}(x-3)+5$
もう1つの接線は $x=3$ であることは図形的にわかる。
よって, 求める接線は, $8x-15y+51=0$ , $x=3$

判別式＝0

解法②判別式＝0
求める直線を $y=m(x-3)+5$ とおいて, $x^2+y^2=9$ に代入すると,
$x^2+\left\{m(x-3)+5\right\}^2=9$
$(1+m^2)x^2-2(3m^2-5m)x+9m^2-30m+16=0$
$D/4=0$ とすると,
$(3m^2-5m)^2-(1+m^2)(9m^2-30m+16)=0$
$-30m+16=0$
$m=\dfrac{8}{15}$
このとき, 求める求める接線の1つは, $y=\dfrac{8}{15}(x-3)+5$
もう1つの接線は $x=3$ であることは図形的にわかる。
よって, 求める接線は, $8x-15y+51=0$ , $x=3$

このようにこの2つの解法では $m$ の値は1つしか出てこないので注意が必要です。答えが出たから安心というわけではなく, もう1つの接線の存在を忘れないようにしたいものです。

接線の公式を利用

最後にこの方法なら2つ出てくるという方法を示しておきます。
解法③接線の公式を利用する方法
円 $x^2+y^2=9$ 上の接点をP $(x_0, y_0)$ とおくと,
接線の方程式は $x_0x+y_0y=9$ と置ける。これが(3,5)を通るので,
$3x_0+5y_0=9\cdots\textcircled{\scriptsize 1}$ が成り立つ。
またP $(x_0, y_0)$ は円上の点なので,
$x_0^2+y_0^2=9\cdots\textcircled{\scriptsize 2}$
$\textcircled{\scriptsize 1}$ を $3x_0=9-5y_0$ として,両辺2乗すると,
$9x_0^2=(9-5y_0)^2\cdots\textcircled{\scriptsize 3}$
$\textcircled{\scriptsize 2}$ を9倍して,
$9x_0^2+9y_0=81$ として, $\textcircled{\scriptsize 3}$ を代入すると,
$(9-5y_0)^2+9y_0^2=81$
整理していくと,
$34y_0^2-90y_0=0$
$2y_0(17y_0-45)=0$
$y_0=0, \dfrac{45}{17}$
$y_0=0$ のとき, $\textcircled{\scriptsize 1}$ から $x_0=3$
このとき接線の方程式は, $3x=9$ , $x=3$
$y_0=\dfrac{45}{17}$ のとき, $\textcircled{\scriptsize 1}$ から $x_0=-\dfrac{24}{17}$
このとき接線の方程式は $-\dfrac{24}{17}x+\dfrac{45}{17}y=9$
以上から, 求める接線は
$x=3$ , $8x-15y+51=0$

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル