こんにちは。今回は等比数列ar^{n-1}の和の公式の導出です。
等比数列の和の公式
初項![]() , 公比
, 公比![]() の等比数列の和の公式は以下になります。
の等比数列の和の公式は以下になります。
等比数列の和の公式
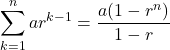 (主に公比
(主に公比もしくは,
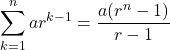 (主に公比
(主に公比公式の導出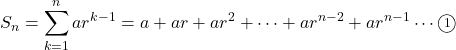
として, ![]() の両辺に公比
の両辺に公比![]() をかけると,
をかけると, 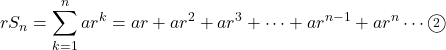
![]() より,
より, 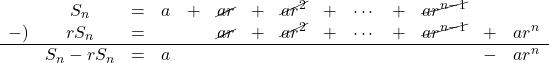
したがって, ![]()
両辺を![]() で割って,
で割って, ![]()
もう1つの公式は右辺の分母分子に![]() をかけて
をかけて![]()
となる。
こんにちは。今回は等比数列ar^{n-1}の和の公式の導出です。
等比数列の和の公式
初項![]() , 公比
, 公比![]() の等比数列の和の公式は以下になります。
の等比数列の和の公式は以下になります。
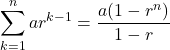 (主に公比
(主に公比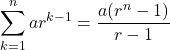 (主に公比
(主に公比公式の導出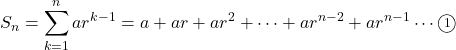
として, ![]() の両辺に公比
の両辺に公比![]() をかけると,
をかけると, 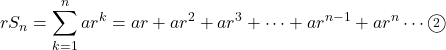
![]() より,
より, 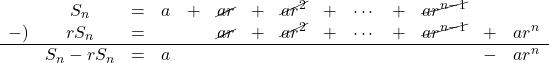
したがって, ![]()
両辺を![]() で割って,
で割って, ![]()
もう1つの公式は右辺の分母分子に![]() をかけて
をかけて![]()
となる。