こんにちは。今回は等差数列の和のところでよく出てくる, 1~![]() までの整数和を求めてみたいと思います。
までの整数和を求めてみたいと思います。
1~nの自然数和の公式
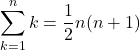
私の覚え方:連続する2数の半分![]()
先ずは一般的な公式の導出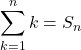 とすると,
とすると, ![]()
この和の順番を逆にすると, ![]()
![]() より,
より, 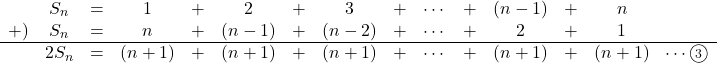
このときできる, ![]() は
は![]() 個できるので,
個できるので, ![]() は次のようになりる。
は次のようになりる。![]()
よって, ![]()
すなわち, 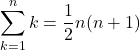
誰が考えた?感心させられる公式の導出
この公式の導出方法を用いて, ![]() の和や
の和や![]() の和の公式も導出できます。知っておくと便利です(記憶違いでなければ数検の準1級で
の和の公式も導出できます。知っておくと便利です(記憶違いでなければ数検の準1級で![]() の和の公式の導出が出ました)。それではいきましょう。
の和の公式の導出が出ました)。それではいきましょう。![]() として辺々の和を1~
として辺々の和を1~![]() までとります。
までとります。
すなわち, 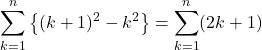
これを![]() から見ていくと
から見ていくと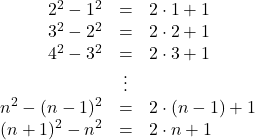
これらをすべて加えると, 2乗の項が打ち消し合っていくことが分かります。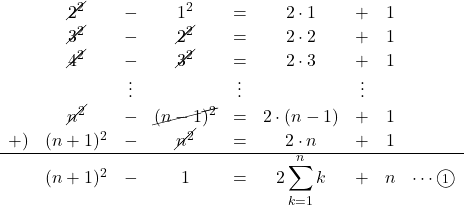
![]() を計算していくと,
を計算していくと, 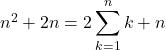
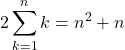
よって, 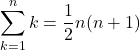
はじめてこの解法を見たとき, えらく感心しました。
それでは。
 数樂管理人のブログ
数樂管理人のブログ 

