こんにちは。![]() 乗根の計算に触れておきます。ここでは以下の決まりにしたがって, 解答してみます。
乗根の計算に触れておきます。ここでは以下の決まりにしたがって, 解答してみます。
累乗根の決まりと性質
累乗根の決まりと性質
正の数 の
の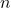 乗根は
乗根は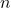 回かけると
回かけると にもどるので, 次の決まりが成り立ちます。
にもどるので, 次の決まりが成り立ちます。
![Rendered by QuickLaTeX.com \left(\sqrt[n]{a}\right)^n=\sqrt[n]{a^n}=a](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-2db06f1d3c7dae6ea6b2272f065b0a86_l3.png) (ただし,
(ただし, 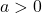 )
)
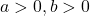 で,
で, 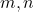 を自然数とすると,
を自然数とすると,
![Rendered by QuickLaTeX.com \begin{array}{clcl} \textcircled{\scriptsize 1}&\sqrt[n]{\mathstrut a}\sqrt[n]{\mathstrut b}=\sqrt[n]{\mathstrut ab}&\textcircled{\scriptsize 2}&\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\\ \textcircled{\scriptsize 3}&\left(\sqrt[n]{\mathstrut a}\right)^m=\sqrt[n]{\mathstrut a^m}&\textcircled{\scriptsize 4}&\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}\\ \end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-0fdb50f4d648ff13d7af9363734b3dec_l3.png)
が成り立つ。
![Rendered by QuickLaTeX.com \begin{array}{clcl} \textcircled{\scriptsize 1}&\sqrt[n]{\mathstrut a}\sqrt[n]{\mathstrut b}=\sqrt[n]{\mathstrut ab}&\textcircled{\scriptsize 2}&\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\\ \textcircled{\scriptsize 3}&\left(\sqrt[n]{\mathstrut a}\right)^m=\sqrt[n]{\mathstrut a^m}&\textcircled{\scriptsize 4}&\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}\\ \end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-0fdb50f4d648ff13d7af9363734b3dec_l3.png)
が成り立つ。
累乗根の決まりと性質を用いた計算
【例】![Rendered by QuickLaTeX.com \begin{array}{ccc}\textcircled{\scriptsize 1}\hspace{2mm}\sqrt[3]{4}\times\sqrt[3]{2}&=&\sqrt[3]{8}\\&=&\sqrt[3]{2^3}\\&=&2\end{arry}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-1a9e5857a7f85e81a3a49f9470b3b084_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{ccc}\textcircled{\scriptsize 2}\hspace{2mm}\dfrac{\sqrt[4]{243}}{\sqrt[4]{3}}&=&\sqrt[4]{\dfrac{243}{3}}\\&=&\sqrt[4]{81}\\&=&\sqrt[4]{3^4}\\&=&3\end{arry}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-1669dfbf828d9793151242f28e8e92bc_l3.png)
![]()
![]()
こんにちは。![]() 乗根の計算に触れておきます。ここでは以下の決まりにしたがって, 解答してみます。
乗根の計算に触れておきます。ここでは以下の決まりにしたがって, 解答してみます。
累乗根の決まりと性質
![Rendered by QuickLaTeX.com \begin{array}{clcl} \textcircled{\scriptsize 1}&\sqrt[n]{\mathstrut a}\sqrt[n]{\mathstrut b}=\sqrt[n]{\mathstrut ab}&\textcircled{\scriptsize 2}&\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\\ \textcircled{\scriptsize 3}&\left(\sqrt[n]{\mathstrut a}\right)^m=\sqrt[n]{\mathstrut a^m}&\textcircled{\scriptsize 4}&\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}\\ \end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-0fdb50f4d648ff13d7af9363734b3dec_l3.png)
累乗根の決まりと性質を用いた計算
【例】![Rendered by QuickLaTeX.com \begin{array}{ccc}\textcircled{\scriptsize 1}\hspace{2mm}\sqrt[3]{4}\times\sqrt[3]{2}&=&\sqrt[3]{8}\\&=&\sqrt[3]{2^3}\\&=&2\end{arry}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-1a9e5857a7f85e81a3a49f9470b3b084_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{ccc}\textcircled{\scriptsize 2}\hspace{2mm}\dfrac{\sqrt[4]{243}}{\sqrt[4]{3}}&=&\sqrt[4]{\dfrac{243}{3}}\\&=&\sqrt[4]{81}\\&=&\sqrt[4]{3^4}\\&=&3\end{arry}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-1669dfbf828d9793151242f28e8e92bc_l3.png)
![]()
![]()