こんにちは。今回は指数関数と不等式について書いておきます。例題を見ながら書いていきます。
【例①】![]()
【解法】底をそろえる。
底を2でそろえると, ![]()
底が1より大きいので,
指数部を比較して, ![]() (答)
(答)
【例②】![]()
【解法】底を![]() でそろえる。
でそろえる。
底を![]() でそろえると,
でそろえると, ![]()
底![]() が1より小さいので,
が1より小さいので,
指数部を比較して, ![]() (答)
(答)
不等号の向きが変わるのは底を2にしてみるとわかる。
底を2にすると, 与式は![]()
底は1より大きいので, ![]()
よって, ![]() (答)
(答)
指数関数を含む不等式
底をそろえて指数部を比較して解く。 このとき, 次の性質を用いる。 ![]() のとき,
のとき, ![]() なら,
なら, ![]()
![]() のとき,
のとき, ![]() なら,
なら, ![]()
続いての例題
【例③】方程式![]() を解きなさい。
を解きなさい。
【解法】これも底をそろえて解いていきます。![]() なので, 底を3として式を書くと,
なので, 底を3として式を書くと,![]()
![]()
![]() とおくと,
とおくと,![]()
![]()
![]() より,
より,![]()
![]() なので,
なので,![]()
![]()
![]() (答)
(答)
【例④】方程式![]() を解きなさい。
を解きなさい。
【解法】これも底をそろえて解いていきます。![]() なので, 底を3として式を書くと,
なので, 底を3として式を書くと,![]()
![]()
![]() とおくと,
とおくと,![]()
![]()
![]() なので,
なので, ![]() より,
より,![]()
![]() なので,
なので,![]()
![]()
![]()
底は1より大きいので, ![]() (答)
(答)
【例⑤】方程式![]() を解きなさい。
を解きなさい。
【解法】これも底をそろえて解いていきます。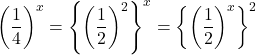 なので, 底を
なので, 底を![]() として式を書くと,
として式を書くと,![]()
![]()
![]() とおくと,
とおくと, ![]()
![]()
![]()
![]() なので,
なので, ![]() ,
, ![]()
![]() ,
, ![]()
底![]() が1より小さいので,
が1より小さいので, ![]() (答)
(答)
指数関数を含む不等式
![]() 底をそろえて
底をそろえて![]() として,
として, ![]() の不等式をつくる。
の不等式をつくる。![]() このとき,
このとき, ![]() なので,
なので, ![]() に気を付けて不等式を解く。
に気を付けて不等式を解く。![]()
![]() なら,
なら, ![]() なので, このようなことから,
なので, このようなことから, ![]() の範囲を求める。
の範囲を求める。
このとき, 底![]() が1より大きいとき, 1より小さいときで不等号の向きに気を付けること。
が1より大きいとき, 1より小さいときで不等号の向きに気を付けること。
 数樂管理人のブログ
数樂管理人のブログ 

