こんにちは。今回は指数関数を含む関数の最大値と最小値について書いておきます。例題を見ながら書いていきます。
a^x=tとおいてtの関数で考える
【例題】関数![]() の最大値と最小値を求め, そのときの
の最大値と最小値を求め, そのときの![]() の値を答えよ。
の値を答えよ。
【解法】![]() なので,
なので, ![]() と置くと, 与式の関数は,
と置くと, 与式の関数は, ![]()
![]()
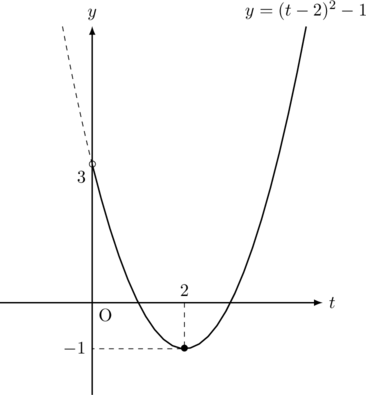
これを平方完成すると, ![]()
定義域![]() において, 最小値は,
において, 最小値は, ![]() のとき,
のとき, ![]() で, 最大値は
で, 最大値は![]() の値が決まらないので, なしになる。
の値が決まらないので, なしになる。![]() はすなわち,
はすなわち, ![]() の事なので, これから最小値を与える
の事なので, これから最小値を与える![]() の値は
の値は![]() と分かる。
と分かる。
よって, ![]() のとき, 最小値
のとき, 最小値![]() , 最大値は, なし
, 最大値は, なし![]() (答)
(答)
【例題】関数![]() の最大値と最小値を求め, そのときの
の最大値と最小値を求め, そのときの![]() の値を答えよ。
の値を答えよ。
【解法】![]() なので,
なので,![]() とおくと, 定義域も変わるので, それを求めると,
とおくと, 定義域も変わるので, それを求めると, ![]()
このとき,与式の関数は, ![]()
![]()
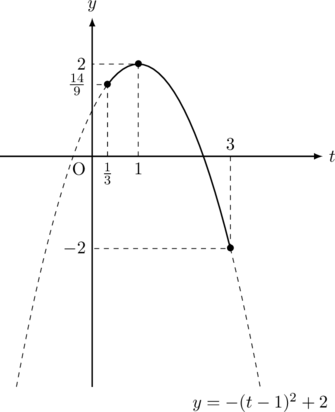
定義域![]() において,
において,
最大値は![]() のとき2で, 最小値は
のとき2で, 最小値は![]() のとき
のとき![]() となる。
となる。
最大値は
最小値は
よって, 最大値は
指数関数を含む関数の最大値・最小値
 数樂管理人のブログ
数樂管理人のブログ 

