TikZ：高校数学：指数と対数の関係・対数とは

こんにちは。今回は指数と対数について書いておきます。

指数と対数・対数とは

対数とは
$a^x=M$ とある場合, この式の意味を言葉で書くと,
$a$ の $x$ 乗が $M$ である。
となります。
指数のところで $a$ のことを底と呼んでいましたが, 対数の分野でもそれは同じです。 $M$ の真数といい, $x$ のことを対数といいます。
具体例で行くと, 2を $x$ 乗すると8になるという言葉を式に書くと,
$2^x=8$
となります。このとき, 対数 $x$ の値は3となります。
つまり, 底を2としたときの8の対数は3になると言えます。
ちなみに, 底を5としたときの25の対数は2になります。

それでは, 2を $x$ 乗して5になるということを考えてみます。
つまり,
$2^x=5$
を満たす $x$ の値を求めることを考えるのですが, この値は $\sqrt3$ (2乗して3になる数)を考えるのと同じで, 存在しません(証明はこちら)。そこで, 対数を表す数学記号 $\log$ を用いて求めることにします。
$2^x=5$ の両辺を底を2とした対数 $\log_2$ をとると
$\log_2{2}^x=\log_2{5}$
$x=\log_2{5}$
となります。
ちなみに, この $\log_2{5}$ の値を電卓で計算すると,
$\log_2{5}=2.321928095\cdots$
つまり
$2^{\log_2{5}}=2^{2.321928095\cdots}=5$
底を2としたときの5の対数は $\log_2{5}$ ということです。
指数関数 $y=2^x$ でどのあたりにあるか確認してみましょう。

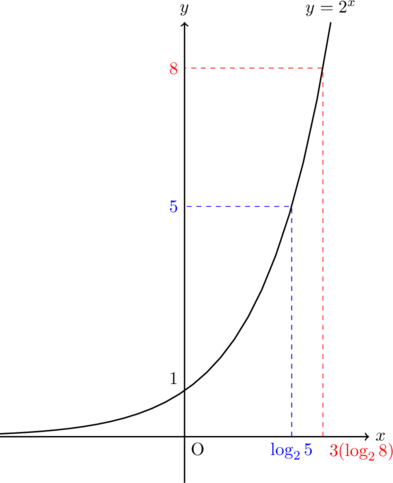
対数

$a>0, a\neq1$ で, $M>0$ とするとき,
$M=a^x\Longleftrightarrow x=\log_a{M}$ (対数の定義)
$a$ を何乗したら $M$ になるか表した数 $x$ を対数と言います。
言い換えると, 底を $a$ としたときの $M$ の対数を $x$ , と言えます。

指数と対数・対数とは

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル