こんにちは。今回は対数の大小関係について書いておきます。例題を見ながら行きましょう。
【例①】![]() の大小関係を不等号を用いて表せ。
の大小関係を不等号を用いて表せ。
【解法】底をそろえて真数部の大小を考える。
この場合, 底を3にそろえて, ![]()
底が1より大きいので, ![]()
したがって, ![]()
【例②】![]() ,
, ![]() ,
, ![]()
【解法】底をそろえて真数部の大小を考える。底が1より小さいことに気を付ける。![]()
![]()
底が1より小さいので, ![]()
したがって, ![]()
対数の大小関係
底![]() をそろえて考える。
をそろえて考える。![]()
![]() のとき,
のとき, ![]() は単調増加のグラフなので,
は単調増加のグラフなので,![]() の値が大きければ
の値が大きければ![]() の値も大きい。
の値も大きい。
したがって, ![]()
![]()
![]() のとき,
のとき,![]() は単調減少のグラフなので,
は単調減少のグラフなので, ![]() の値が大きければ
の値が大きければ![]() の値は小さい。
の値は小さい。
したがって, ![]()
【例③】![]() ,
, ![]() ,
, ![]() の大小関係を不等号を用いて表せ。
の大小関係を不等号を用いて表せ。
【解法】底を真数にして底変換を行う。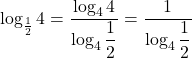
![]()
![]()
ここで, ![]() であるから,
であるから, ![]()
また, 底が1より大きいので![]() なので,
なので, ![]()
以上より, ![]()
真数がそろってる
底を真数の値にして底変換して, 大小関係を調べるのがコツ。
【例④】![]() と
と![]() の大小関係を不等号を用いて表せ。
の大小関係を不等号を用いて表せ。
【解法】まず, ![]() を底を10とした対数で表す。
を底を10とした対数で表す。![]()
![]() となり, 底が1より大きいので, 真数部分の大小を考えればよい。
となり, 底が1より大きいので, 真数部分の大小を考えればよい。
つまり, ![]() と
と![]() の大小を考えるとよい。
の大小を考えるとよい。
ここで, この2数を考えやすくするために, それぞれ10乗すると, ![]() ,
, ![]() となり,
となり, ![]() となる。
となる。
つまり, ![]() である。
である。
ゆえに, ![]()
 高校数学:対数:テクニックは不要の対数の大小(高知大)
高校数学:対数:テクニックは不要の対数の大小(高知大) 数樂管理人のブログ
数樂管理人のブログ 

