こんにちは。今回は対数の性質とその証明について書いておきます。
対数の性質
![]() とすると,
とすると,![]()
![]()
![]()
![]()
![]()
![]() 【
【![]() 乗⇔
乗⇔![]() 倍】
倍】![]()
![]() 【積⇔和】
【積⇔和】![]()
![]() 【商⇔差】
【商⇔差】![]()
![]() 【底の変換公式】
【底の変換公式】
特に![]() なら,
なら, ![]()
が成り立つ。
まず, 対数の定義のおさらい。![]() において,
において, ![]()
を定義する
対数の性質の証明![]()
![]()
対数の定義 ![]() において,
において, ![]() とすると,
とすると, ![]()
つまり, ![]() となるので,
となるので, ![]() となる。
となる。
![]()
![]()
対数の定義 ![]() において,
において, ![]() とすると,
とすると,![]()
つまり, ![]() となるので,
となるので,![]() となる。
となる。
![]()
![]() 【
【![]() 乗⇔
乗⇔![]() 倍】
倍】
対数の定義![]() から,
から, ![]() として, 両辺
として, 両辺![]() 乗すると,
乗すると, ![]()
ここで, 底を![]() とする対数をとると,
とする対数をとると, ![]()
![]()
先の定義より![]() なので,
なので, ![]()
![]()
![]() 【積⇔和】
【積⇔和】![]() ,
, ![]() とすると,
とすると, ![]() ,
, ![]() となる。
となる。
このとき, 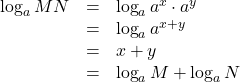
![]()
![]() 【商⇔差】
【商⇔差】![]() ,
, ![]() とすると,
とすると,![]() ,
, ![]() となる。
となる。
このとき,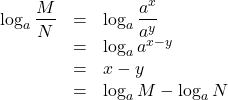
![]()
![]() 【底の変換公式】
【底の変換公式】
対数の定義より, ![]() であるから,
であるから, ![]() の両辺に底を
の両辺に底を![]() とする対数をとると,
とする対数をとると, ![]()
![]()
![]()
定義より, ![]() なので, これで置き換えると,
なので, これで置き換えると, ![]()
また, このとき, ![]() とすると,
とすると, 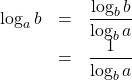
が成り立つ。
 数樂管理人のブログ
数樂管理人のブログ 

