TikZ：高校数学：対数関数とグラフ

こんにちは。今回は対数のグラフについて書いておきます。

対数関数とグラフ

$a>0, a\neq1$ のとき, $y=\log_a x$ を $a$ を底とする対数関数と言います。対数関数は指数関数 $y=a^x$ と関数 $y=x$ について対称な関係にあります。
これは, 対数関数と指数関数が逆関数の関係にあるためで, 逆関数というのは簡単に言えば,
$y=f(x)$ で, $x=a$ のとき, $y=b$ であったものが, 逆関数 $y=g(x)$ では $x=b$ のとき, $y=a$ となるためです。詳しくは数Ⅲで学習します。
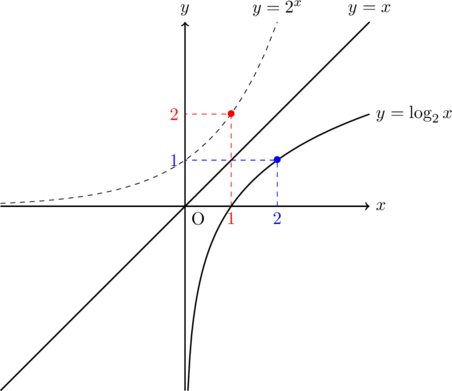
以下に底が1より大きい場合として, $y=\log_2 x$ , $y=2^x$ のグラフを描いてみます。赤丸と青丸の座標は $y=x$ について対称になっています。

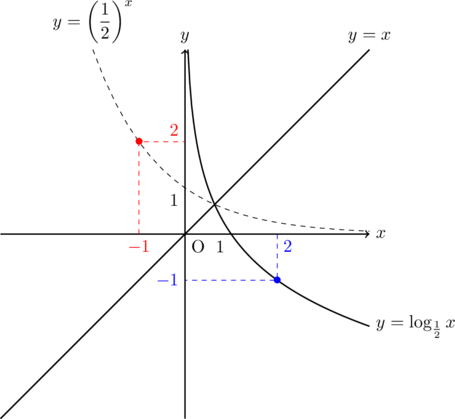
次に底が1より小さい場合を描いてみます。
$y=\log_{\frac12}x$ と $y=\left(\dfrac12\right)^x$ のグラフです。赤丸と青丸の座標は $y=x$ について対称になっています。

このとき, $y=\log_p x$ と $y=\log_{\frac1p} x$ 　 $(p>1)$ とするなら, この2つのグラフは $x$ 軸について対象な関係になっています。

対数関数のグラフについて

$a>0, a\neq1$ のとき, $y=\log_a x$ のことを, $a$ を底とする対数関数という。
$\textcircled{\scriptsize 1}\hspace{2mm}a>1$ (底が1より大きい)のとき, 右上がりの曲線
$\textcircled{\scriptsize 2}\hspace{2mm}0<a<1$ (底が0と1の間の数)のとき, 右下がりの曲線となる。
このとき, $\textcircled{\scriptsize 1}, \textcircled{\scriptsize 2}$ とも $y$ 軸が漸近線である。漸近線とは, 十分遠くで曲線との距離が0に近づき, かつ曲線と一致しない直線のことを指す。

対数関数とグラフ

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル