こんにちは。今回は対数関数を含む関数の最大値・最小値について書いておきます。例題を解きながら見ていきます。
【例】関数![]()
![]() の最大値と最小値を求め, そのときの
の最大値と最小値を求め, そのときの![]() の値も答えよ。
の値も答えよ。
【解法】![]() と置くと,
と置くと, ![]() である。
である。
また, 関数は![]() となるので, 平方完成すると,
となるので, 平方完成すると, ![]()
![]()
グラフを描いて, 最大値, 最小値を求めると,
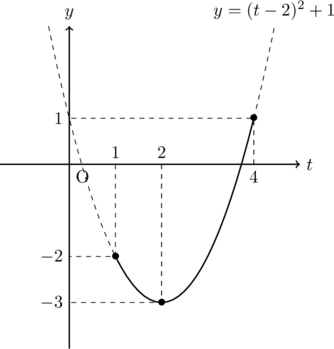
最小値は
よって,
最小値は
最大値は
対数を含む二次不等式について
![]()
![]() と置いて
と置いて![]() の関数をつくる。
の関数をつくる。![]()
![]() の定義域から,
の定義域から, ![]() の定義域を求める。
の定義域を求める。![]() グラフを描いて最大値, 最小値を求める。
グラフを描いて最大値, 最小値を求める。![]() 必要なら, 最大値, 最小値を与える
必要なら, 最大値, 最小値を与える![]() の値から,
の値から, ![]() の値を求める。
の値を求める。
 数樂管理人のブログ
数樂管理人のブログ 

