こんにちは。今回は常用対数と桁数の関連について書いておきます。例題を解きながら見ていきましょう。
【例①】自然数![]() が次の桁数のとき,
が次の桁数のとき, ![]() の範囲を求めなさい。
の範囲を求めなさい。
(1) 3桁 (2) 12桁
【解法】
(1) 3桁ということは自然数![]() の範囲は
の範囲は![]() となります。
となります。
この不等式の各辺の常用対数をとると, ![]()
![]()
![]() (答)
(答)
(2) 12桁ということは自然数![]() の範囲は
の範囲は![]()
この不等式の各辺の常用対数をとると, ![]()
![]() (答)
(答)
このように自然数![]() が
が![]() 桁の数であるなら,
桁の数であるなら, ![]() の範囲は
の範囲は![]() の範囲になります。
の範囲になります。
これに対して, 各辺の常用対数をとると, ![]()
![]()
つまり, 自然数![]() が
が![]() 桁
桁![]()
常用対数と桁数
自然数![]() が
が![]() 桁
桁![]()
【例②】![]() は何桁の数か,
は何桁の数か, ![]() として, 計算せよ。
として, 計算せよ。
【解法】![]() として, 両辺の常用対数をとると,
として, 両辺の常用対数をとると, 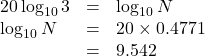
これより, ![]() なので,
なので,
10桁の数となります。
常用対数と桁数
![]() 求める自然数が
求める自然数が![]() のとき, その常用対数をとる。
のとき, その常用対数をとる。 ![]() 与えられている数値をもとに
与えられている数値をもとに![]() を計算する。
を計算する。![]()
![]() 自然数
自然数![]() が
が![]() 桁を用いて何桁か求める。
桁を用いて何桁か求める。
 数樂管理人のブログ
数樂管理人のブログ 

