高校数学：常用対数と小数の桁数

こんにちは。今回は常用対数と小数の桁数について書いておきます。例題を解きながら見ていきましょう。

常用対数と小数

先ず, 小数第2位で初めて0でない数が現れる数 $M (0<M<1)$ があるとしたら, その数 $M$ とはどんな範囲にあるかというと,
$0.01\leqq M<0.1\Leftrightarrow10^{-2}\leqq M<10^{-1}$
という範囲にあることが分かります。
同じように, 小数第5位で初めて0でない数が現れるとしたら, その数 $M (0<M<1)$ はどんな範囲かというと,
$0.00001\leqq M<0.00001\Leftrightarrow10^{-5}\leqq M<10^{-4}$
という範囲になります。
これを一般的に見ていくと,
小数第 $n$ 位に初めて0でない数が現れるとき, $M$ の範囲は,
$10^{-n}\leqq M<10^{-(n-1)}$
となり, 各辺の常用対数をとると,
$\log_{10}10^{-n}\leqq \log_{10}M<\log_{10}10^{-(n-1)}$
$-n\leqq \log_{10}M<-(n-1)$
つまり, これを一般化していくと, 次の事が言えます。
小数 $M$ 　 $(0<M<1)$ が, 小数第 $n$ 位初めて0でない数が現れる $\Longleftrightarrow -n\leqq \log_{10}M<-(n-1)$
これを使って, 問題を解いていきます。

常用対数と小数

小数 $M$ 　 $(0<M<1)$ が, 小数第 $n$ 位初めて0でない数が現れる $\Longleftrightarrow -n\leqq \log_{10}M<-(n-1)$

常用対数と小数の例題

【例】 $\left(\dfrac12\right)^{20}$ を小数で表したとき, 小数第何位に初めて0でない数が現れるか答えよ。ただし, $\log_{10}2=0.3010$ として計算すること。
【解法】
$\left(\dfrac12\right)^{20}=M$ として, 両辺の常用対数をとると,
$\begin{array}{lll}20\log_{10}\dfrac12&=&\log_{10}M\\\log_{10}M&=&20\log_{10}2^{-1}\\&=&-20\log_{10}2\\&=&-20\times0.3010\\&=&-6.02\end{array}$
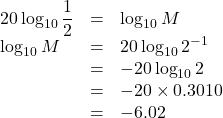
$-7<\log_{10}M(-6.02)<-6$ なので,
小数第7位に初めて0でない数が現れる。

常用対数と桁数

$\textcircled{\scriptsize 1}$ 　求める小数が $M=a^x$ のとき, その常用対数をとる。
$\textcircled{\scriptsize 2}$ 　与えられている数値をもとに $\log_{10}N$ を計算する。
$\textcircled{\scriptsize 3}$ 　 $-n\leqq \log_{10}M<-(n-1)\Longleftrightarrow$ 小数 $M$ が小数第 $n$ 位で初めて0でない数が現れるを用いて解く。

常用対数と小数

常用対数と小数の例題

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル