こんにちは。今回は常用対数について少しだけ書いて, 計算練習しておきます。
常用対数とは底を10とした場合の対数のことを言います。すなわち10を何乗すればその値になるかを表したものになります。![]()
![]() の両辺を底を10として対数をとると,
の両辺を底を10として対数をとると, ![]()
具体例を書くと, ![]()
となります。
常用対数
![]() とするとき,
とするとき,![]() (対数の定義から)
(対数の定義から)![]() を何乗したら
を何乗したら![]() になるか表した数
になるか表した数![]() を常用対数と言います。
を常用対数と言います。
言い換えると, 底を![]() としたときの
としたときの![]() の常用対数を
の常用対数を![]() , と言えます。
, と言えます。
こちらに常用対数の表を置いておきます。
常用対数の表の見方は以下の画像をご参照ください。例として1.53の常用対数を示しています。この場合, 0.1847が常用対数になります。
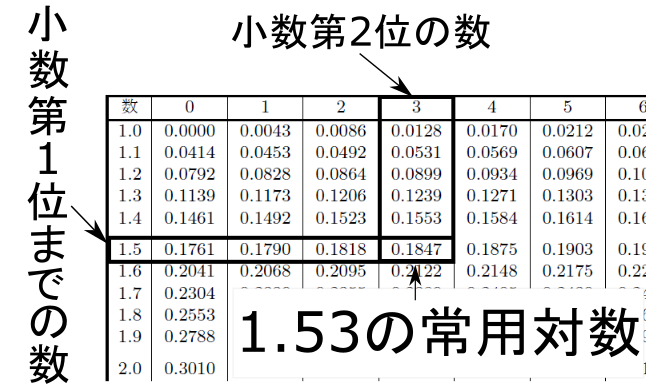
次に常用対数を使った計算を書いておきます。
例題を見ながら書いておきます。
【例】![]() として,
として, ![]() ,
, ![]() の値を小数第4位まで求めなさい。
の値を小数第4位まで求めなさい。
【解法】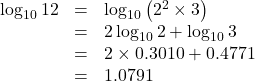
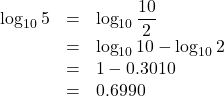
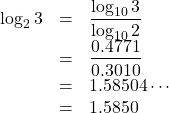
対数の性質
![]() とすると,
とすると,![]()
![]()
![]()
![]()
![]()
![]() 【
【![]() 乗⇔
乗⇔![]() 倍】
倍】![]()
![]() 【積⇔和】
【積⇔和】![]()
![]() 【商⇔差】
【商⇔差】![]()
![]() 【底の変換公式】
【底の変換公式】
特に![]() なら,
なら, ![]()
が成り立つ。
 数樂管理人のブログ
数樂管理人のブログ 

