こんにちは。今回は弧度法について書いてきます。
弧度法とは
半径![]() の扇形の弧の長さ
の扇形の弧の長さ![]() は扇形の中心角
は扇形の中心角![]() の大きさに比例する。これは扇形の半径
の大きさに比例する。これは扇形の半径![]() と弧の長さ
と弧の長さ![]() がわかれば, その中心角
がわかれば, その中心角![]() は分かるということを意味します。そこで, この
は分かるということを意味します。そこで, この![]() を
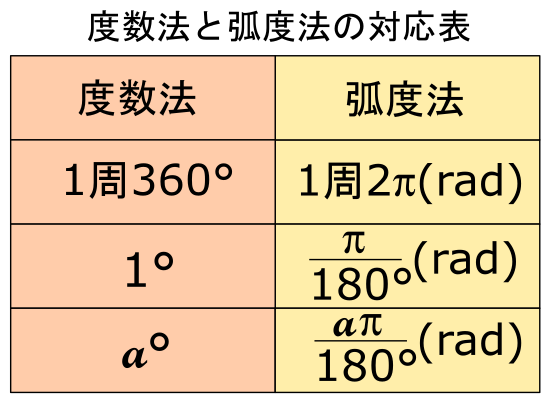
を![]() (rad) (単位はラジアンと呼ぶ)
(rad) (単位はラジアンと呼ぶ)
として定義します。この角度の表し方を弧度法と言います。ただ, 単位は省くことが多いです。
今まで扱ってきた, 45![]() , 180
, 180![]() などは度数法と言います。
などは度数法と言います。
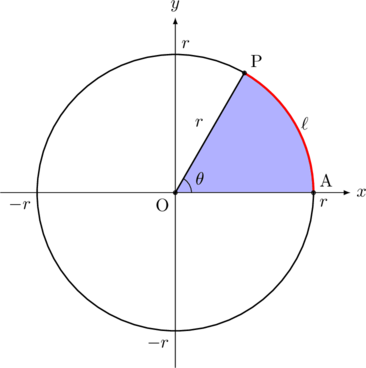
具体例を見てみる
それでは実際に数字で追っかけてみましょう。
半径2, 中心角60![]() なら
なら![]() (rad)はいくらになるのでしょうか。
(rad)はいくらになるのでしょうか。
このとき, 弧の長さ![]() は,
は, 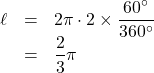
弧度法の定義より, このときの角![]() (rad)は,
(rad)は, 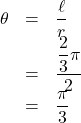
となり, ![]() (rad)となり,
(rad)となり,
これは度数法では![]() なので,
なので, ![]() (rad)
(rad)
が成り立ちます。
半径1にすれはℓが弧度θになる
先ほど, 半径2でやりましたが, 半径1にすれば, ![]() となるので, 弧の長さ
となるので, 弧の長さ![]() が直接
が直接![]() (rad)になります。つまり,
(rad)になります。つまり, ![]() (rad)
(rad)
となります。
ここで, 半径1の円の円周を考えると, 円1周が何radか知れるので計算すると, ![]() (rad)
(rad)
これは, 度数法でいうと, 360![]() にあたるので,
にあたるので, ![]() (rad)
(rad)
という関係ができ, 両辺を360![]() で割ると,
で割ると, ![]() (rad)
(rad)![]()
逆に両辺を2![]() で割ると,
で割ると, ![]() (rad)
(rad)![]()
となります。
また, ![]() (rad),
(rad), ![]() (rad)
(rad)
となります。
実際扱うときは, ![]() (rad)を用いて解いていきます。
(rad)を用いて解いていきます。
度数法を弧度法に
【例①】45![]() , 90
, 90![]() , 120
, 120![]() を弧度法に書き直しなさい。
を弧度法に書き直しなさい。
【解法】それぞれ![]() をかけると求まる。
をかけると求まる。
45![]() は,
は, ![]()
80![]() は,
は, ![]()
120![]() は,
は, ![]()
感覚的には180![]() で割るイメージ。
で割るイメージ。
弧度法を度数法に
【例②】![]() ,
, ![]() ,
, ![]() を弧度法に書き直しなさい
を弧度法に書き直しなさい
【解法】それぞれ, ![]() を180
を180![]() に置き換えてかけると求まります。
に置き換えてかけると求まります。![]() は,
は, ![]()
![]() は,
は, ![]()
![]() は,
は, ![]()
感覚的には180![]() をかけるイメージ。
をかけるイメージ。
 数樂管理人のブログ
数樂管理人のブログ 

