TikZ：高校数学：180°を越える三角関数

2021年5月3日2022年5月2日

SHARE

こんにちは。今回は180 $^{\circ}$ を越える場合の三角関数について書いておきます。

高1と何ら変わらない

三角関数の定義は次のようでした。
以下のような半径 $r$ の円があって, その円周上の点をP( $x$ , $y$ )とする。 $\angle{\text{AOP}}=\theta$ とするとき, $\sin\theta$ , $\cos\theta$ , $\tan\theta$ は以下の式で求められます。

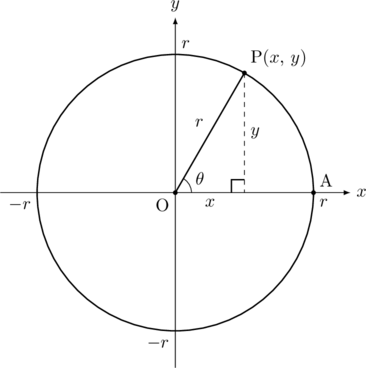
定義

$\sin\theta=\dfrac{y}{r},\ \cos\theta=\dfrac{x}{r},\ \tan\theta=\dfrac{r}{x}$

ただし, $\theta=90^{\circ}, 270^{\circ}$ など, Pが $y$ 軸にくる場合では, $\tan\theta$ は定義されない(分母が0になるため)とする。

例題をやってみる

今回この定義が引き継がれることになります。したがって, $\theta=240^{\circ}$ とした場合を考えると, 次のように円を書いて考えることになります。

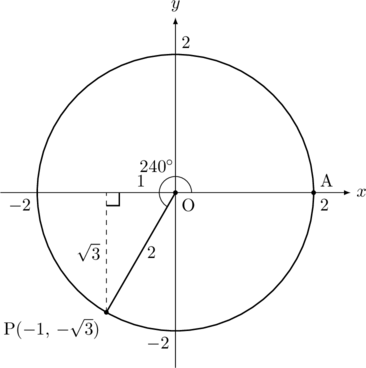
このとき, 点Pの座標は, P $(-1, -\sqrt3)$ , 半径は2, 定義より,
$\sin\theta=\dfrac{y}{r},\ \cos\theta=\dfrac{x}{r},\ \tan\theta=\dfrac{r}{x}$ であるから,
$\sin240^{\circ}=-\dfrac{\sqrt3}{2}$
$\cos240^{\circ}=-\dfrac{1}{2}$
$\tan240^{\circ}=\dfrac{-\sqrt3}{-1}=\sqrt3$

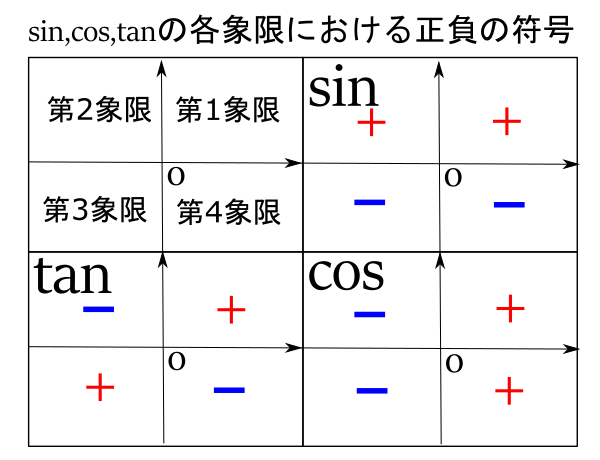
各象限でのsin,cos,tanの符号

また, 各象限での $\sin, \cos, \tan$ の符号は次のようになります。

コメントを残すコメントをキャンセル

前の記事

TikZ：高校数学：弧度法について

次の記事

TikZ：高校数学：θが－θになった場合の三角関数