TikZ：高校数学：θが－θになった場合の三角関数

今回は $\theta$ が $-\theta$ となる場合, $\sin,\cos,\tan$ の値はどう変わるか書いておきます。

θが－θになると

このような関係は単位円もしくは, 円を書いて考えるとすっきりする。このような仕組みを理解しておくと, 公式を覚えなくても済むので, よいと思う。ただ, 公式を覚えらる人は覚えた上で, 忘れたときの保険として, 仕組みを理解しておくことをお勧めする。

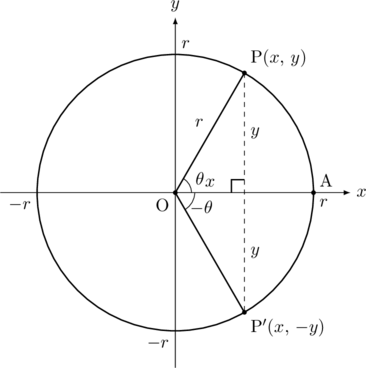
上の図では, 動径OPと動径OP $'$ は $x$ 軸について対称な関係にあるので, PとP $'$ の座標の違いは, $y$ 座標の符号だけである。
したがって, $\sin\theta, \cos\theta, \tan\theta$ で考えれば, $y$ 座標が関係するのは, $\sin\theta, \tan\theta$ なので, $-\theta$ とした場合, $\sin\theta, \tan\theta$ の2つの符号が変わることになる。 $\cos\theta$ の値は $-\theta$ としても変わらないということである。
つまり,
$\sin\left(-\theta\right)=-\sin\theta$
$\cos\left(-\theta\right)=\cos\theta$
$\tan\left(-\theta\right)=-\tan\theta$
となる。

θが－θになった場合

$\sin\left(-\theta\right)=-\sin\theta$
$\cos\left(-\theta\right)=\cos\theta$
$\tan\left(-\theta\right)=-\tan\theta$

【GOM Mix】初心者でも簡単な動画編集ソフト

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル