こんにちは。今回は三角関数の不等式の第2弾ということで書いておきます。例題を解きながら見ていきますね。
θの範囲に注意する
【例①】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】基本的な解き方は不等式①の解き方でいいのですが, ![]() の部分が少々複雑です。
の部分が少々複雑です。![]() の範囲で答えを考えなくてはいけないので, 問題にある,
の範囲で答えを考えなくてはいけないので, 問題にある, ![]() の各辺から
の各辺から![]() を引くと,
を引くと, ![]() となり, この範囲で, 解を考えることになります。ここで,
となり, この範囲で, 解を考えることになります。ここで, ![]() と置くと,
と置くと, ![]() ,
, ![]() となり, 従来の解き方に帰着します。
となり, 従来の解き方に帰着します。![]() の範囲から,
の範囲から, ![]() となる
となる![]() の値は,
の値は, ![]() となり,
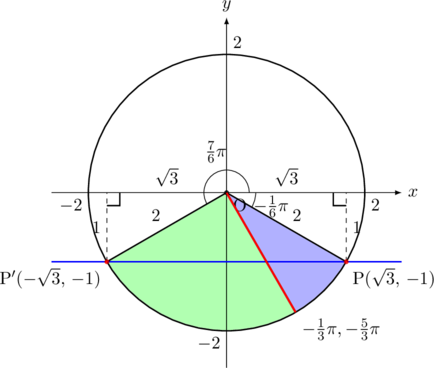
となり, ![]() の値の大小は
の値の大小は![]() 座標が決めるので, それより小さい範囲を考える。
座標が決めるので, それより小さい範囲を考える。 ![]() の範囲が
の範囲が![]() (下図赤線部)からということを考えると, 下図で色分けした部分が求める範囲になる。
(下図赤線部)からということを考えると, 下図で色分けした部分が求める範囲になる。
したがって, ![]() の範囲は,
の範囲は, ![]()
![]() を元に戻して,
を元に戻して, ![]()
よって, ![]() (答)
(答)
【例②】![]() のとき, 方程式
のとき, 方程式![]() を解け。
を解け。
【解法】この場合, 上と異なるのは![]() の部分になる。
の部分になる。![]() となっているので, 問題の
となっているので, 問題の![]() の範囲をそれに合わせるために, 各辺2倍して
の範囲をそれに合わせるために, 各辺2倍して![]() を加えると,
を加えると, ![]() となり, この範囲で解を考えることになる。
となり, この範囲で解を考えることになる。![]() と置くと,
と置くと, ![]() ,
, ![]() となり, 従来の解き方に帰着します。この範囲で,
となり, 従来の解き方に帰着します。この範囲で, ![]() となる
となる![]() の値を求めると, 下図から,
の値を求めると, 下図から, ![]() となり,
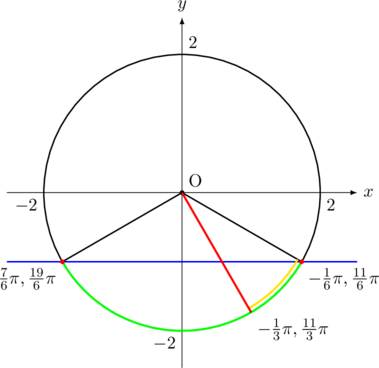
となり, ![]() 座標がそれより, 小さくなる範囲は下図の緑の範囲である。
座標がそれより, 小さくなる範囲は下図の緑の範囲である。![]() の範囲が
の範囲が![]() (下図赤線部)からということを考えると, 下図で色分けした黄色と緑色部分が求める範囲になる。
(下図赤線部)からということを考えると, 下図で色分けした黄色と緑色部分が求める範囲になる。
したがって, ![]() の範囲は,
の範囲は, ![]()
![]() を元に戻して,
を元に戻して, ![]()
これを解いて, ![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 
