こんにちは。今回はベクトルの問題でPの存在範囲というのをやってみます。例題を見ていきましょう。
【例】△OABにおいて, 次の式を満たす点Pの存在範囲を求めよ。![]() ,
, ![]() ,
, ![]()
【解法】先ず, ![]() の範囲において, 各辺を3で割って, 1までの範囲の式をつくる。
の範囲において, 各辺を3で割って, 1までの範囲の式をつくる。![]()
このときできた, ![]() をつかって, ベクトルの式を書き換えると,
をつかって, ベクトルの式を書き換えると, 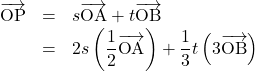
となり, ![]() ,
, ![]() とおくと,
とおくと, ![]() ,
, ![]() ,
, ![]()
このとき, ![]() ,
, ![]() となる点をとると, Pの存在範囲は△OA
となる点をとると, Pの存在範囲は△OA![]() B
B![]() の周及び内部(下図の色を付けた部分, 境界線は含む)となる。
の周及び内部(下図の色を付けた部分, 境界線は含む)となる。

基本的な解法のテクニック
![]() 与えられた
与えられた![]() に関する式から, 両辺を割ることで最大1の範囲の式をつくる。
に関する式から, 両辺を割ることで最大1の範囲の式をつくる。![]()
![]() で得られた〇
で得られた〇![]() , △
, △![]() を用いて, 与式を書き換える。(〇, △は定数)
を用いて, 与式を書き換える。(〇, △は定数)![]()
![]() で書き替えた式から範囲を調べ, 図示する。
で書き替えた式から範囲を調べ, 図示する。
 TikZ:高校数学:ベクトルと点Pの存在範囲2
TikZ:高校数学:ベクトルと点Pの存在範囲2 数樂管理人のブログ
数樂管理人のブログ 

