TikiZ：高校数学：ベクトルと点Pの位置関係(分点公式の応用)

こんにちは。今回は分点の公式を使いこなすことで, 点Pの位置を調べてみましょう。それでは例題を見ていきます。

Pの位置を調べる問題の例

【例】△ABCと点Pに対して, $2\overrightarrow{\text{PA}}+3\overrightarrow{\text{PB}}+4\overrightarrow{\text{PC}}=\overrightarrow{0}$ が成り立つとき, 点Pはどのような位置にあるか調べよ。
【解法】

図を参考にすべて始点をAにして等式を書き換えることにする。
$\overrightarrow{\text{PA}}=-\overrightarrow{\text{AP}}$
$\overrightarrow{\text{PB}}=\overrightarrow{\text{AB}}-\overrightarrow{\text{AP}}$
$\overrightarrow{\text{PC}}=\overrightarrow{\text{AC}}-\overrightarrow{\text{AP}}$
であるから, 与式の等式は次のようになる。
$-2\overrightarrow{\text{AP}}+3\left(\overrightarrow{\text{AB}}-\overrightarrow{\text{AP}}\right)+4\left(\overrightarrow{\text{AC}}-\overrightarrow{\text{AP}}\right)=\overrightarrow{0}$
$-9\overrightarrow{\text{AP}}+3\overrightarrow{\text{AB}}+4\overrightarrow{\text{AC}}=\overrightarrow{0}$
$\overrightarrow{\text{AP}}=\dfrac19\left(3\overrightarrow{\text{AB}}+4\overrightarrow{\text{AC}}\right)$
これを分点の公式 $\dfrac{n\overrightarrow{\mathstrut a}+m\overrightarrow{\mathstrut b}}{m+n}$ が使える形に変形すると,
$\overrightarrow{\text{AP}}=\dfrac79\left(\dfrac{3\overrightarrow{\text{AB}}+4\overrightarrow{\text{AC}}}{7}\right)$
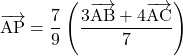
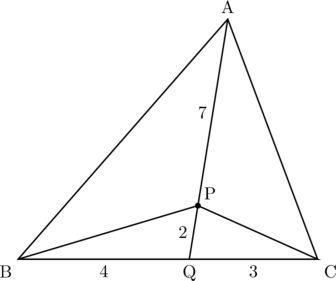
これより, 辺BCを4 : 3に内分する点をQとすると, 点Pは線分AQを7 : 2に内分する点である。下図参照。

流れをつかんでおこう

$\textcircled{\scriptsize 1}$ 　始点を頂点の1つにそろえて等式を書き換える。
$\textcircled{\scriptsize 2}$ 　書き換えた等式をPを含むベクトルについて解く。今回なら $\overrightarrow{\text{AP}}$
$\textcircled{\scriptsize 3}$ 　分点の公式 $\dfrac{n\overrightarrow{\mathstrut a}+m\overrightarrow{\mathstrut b}}{m+n}$ を用いて式変形する。
$\textcircled{\scriptsize 4}$ 　変形した式から位置を読み取る。

Pの位置を調べる問題の例

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル