こんにちは。今回は加法定理の証明ということで, よく書いてあるのが, 単位円を使ったやつですが, 今回は三角形を用いた証明でやってみたいと思います。
加法定理
sinの加法定理の証明
![]() の証明
の証明
下の図のような三角形で, CB![]() , AC
, AC![]() , AB
, AB![]() ,
, ![]() とすると,
とすると,
AD![]() , BD
, BD![]() となる。
となる。
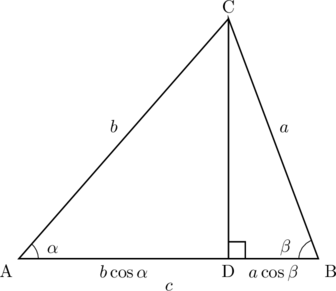
このとき,
また, △ABCに正弦定理を適用すると,
となるので,
これらを
よって,
三角形が鈍角の場合, 下の図のような
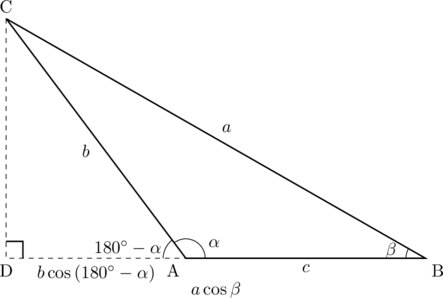
このとき,
となる。以下先と同じ正弦定理を用いて証明する。(割愛)
この証明から, ![]() が得られ,
が得られ,
の![]() を
を![]() に置き換えると,
に置き換えると, ![]()
よって, ![]()
以上より,![]()
cosの加法定理の証明
![]() の証明
の証明![]() の
の![]() を
を![]() に置き換えると,
に置き換えると, ![]()
![]()
よって, ![]()
![]() を
を![]() に置き換えると,
に置き換えると, ![]()
よって, ![]()
以上より, ![]()
tanの加法定理の証明
![]() の証明
の証明![]()
これまでの証明を利用すると, ![]() は次のように書き換えることができる。
は次のように書き換えることができる。 ![]()
右辺の分子分母を![]() で割ると,
で割ると, 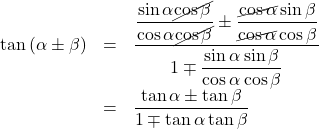
以上より, ![]()
 数樂管理人のブログ
数樂管理人のブログ 

