こんにちは。今回は単位円を使った加法定理の証明を行います。
加法定理
cosの加法定理の証明
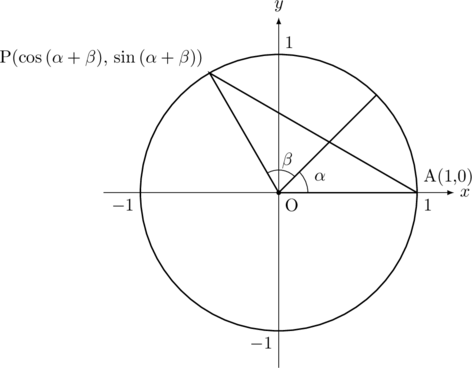
下図の単位円で, 点A( 1, 0 )を![]() 回転させた点Pの座標は,
回転させた点Pの座標は, ![]() となる。
となる。
このとき, 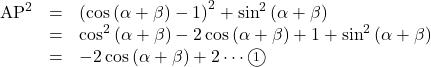
となります。
次にこの△AOPを点Oを回転の中心として,
このとき,
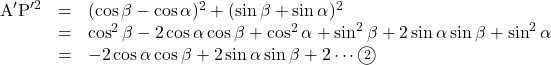
となる。
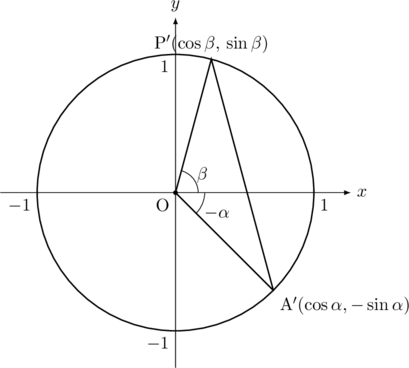
△AOP
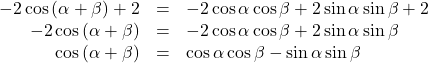
よって,
が成立する。
が得られる。
以上より,
sinの加法定理の証明
![]() で
で![]() を
を![]() とすると,
とすると, 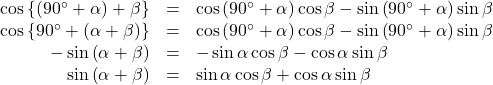
よって, ![]()
が得られ, この式で, ![]() を
を![]() で置き換えると,
で置き換えると, ![]()
![]()
が得られる。
以上より, ![]()
tanの加法定理の証明
![]() の証明
の証明![]()
これまでの証明を利用すると, ![]() は次のように書き換えることができる。
は次のように書き換えることができる。![]()
右辺の分子分母を![]() で割ると,
で割ると,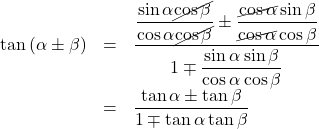
以上より,![]()
 数樂管理人のブログ
数樂管理人のブログ 
