こんにちは。今回はデータの値がすべて![]() 倍されたら, 平均, 偏差, 分散, 標準偏差, 相関係数がどう変わるか見ていきます。
倍されたら, 平均, 偏差, 分散, 標準偏差, 相関係数がどう変わるか見ていきます。
平均
データ![]() の平均を
の平均を![]() とすると,
とすると,![]()
ここで, データをそれぞれ![]() 倍して平均
倍して平均![]() をとると,
をとると,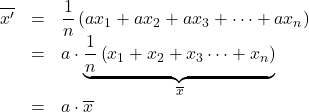
このように, 平均は![]() 倍されることが分かります。
倍されることが分かります。
偏差
偏差はデータと平均との差なので, データは![]() 倍されて, 平均も先の計算から
倍されて, 平均も先の計算から![]() 倍されることから, 偏差は
倍されることから, 偏差は![]() 倍されることが分かります。以下参照ください。
倍されることが分かります。以下参照ください。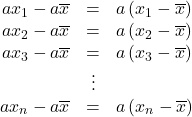
このように右辺の結果は, ![]() 倍されることが分かります。
倍されることが分かります。
分散
分散は偏差の2乗の平均ですから, 元の分散を![]() とすると,
とすると, ![]()
![]() 倍されたデータでは, 偏差が
倍されたデータでは, 偏差が![]() 倍されるので, その分散
倍されるので, その分散![]() は,
は, ![Rendered by QuickLaTeX.com \begin{array}{rcl}s'^2&=&\dfrac{1}{n}\left[\left\{a\left(x_1-\overline{x}\right)\right\}^2+\left\{a\left(x_2-\overline{x}\right)\right\}^2+\left\{a\left(x_3-\overline{x}\right)\right\}^2+\cdots+\left\{a\left(x_n-\overline{x}\right)\right\}^2\right]\\&=&a^2\cdot \underbrace{ \dfrac{1}{n}\left\{\left(x_1-\overline{x}\right)^2+\left(x_2-\overline{x}\right)^2+\left(x_3-\overline{x}\right)^2+\cdots+\left(x_n-\overline{x}\right)^2\right\} }_{\LARGE{s^2}} \\&=&a^2\cdot s^2\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-3edb2e8291f28efaa4d6092b3d0dbb68_l3.png)
したがって, 分散は元の分散の![]() 倍になる。
倍になる。
標準偏差
標準偏差![]() は分散の正の平方根なので,
は分散の正の平方根なので,
分散が![]() 倍されるなら標準偏差は
倍されるなら標準偏差は![]() 倍されます。絶対値が付いてるのは
倍されます。絶対値が付いてるのは![]() の場合を考慮してのことです。
の場合を考慮してのことです。![]() となります。
となります。![]() は元の標準偏差です。
は元の標準偏差です。
相関係数
2つのデータ![]() ,
, ![]() があるとき, 共分散
があるとき, 共分散![]() は次式で与えられます。
は次式で与えられます。![]()
また, それぞれのデータの標準偏差を![]() ,
, ![]() とすると,
とすると,
相関係数![]() は
は![]()
で与えられます。
相関係数を片方のデータ![]() を
を![]() 倍したとき, 両方のデータを
倍したとき, 両方のデータを![]() 倍したときで見ていきます。
倍したときで見ていきます。
【Case1】
片方のデータ![]() を
を![]() 倍したときの共分散
倍したときの共分散![]() は, 平均
は, 平均![]() も
も![]() 倍されるので,
倍されるので, 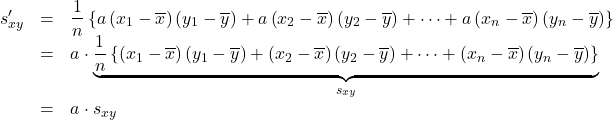
標準偏差は![]() 倍されるので, このときの標準偏差を
倍されるので, このときの標準偏差を![]() とすると,
とすると, ![]()
したがって, このときの相関係数![]() は,
は, 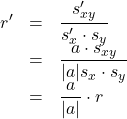
これは, ![]() なら1倍で変化がなく,
なら1倍で変化がなく, ![]() なら
なら![]() 倍で, 元の相関関係の位置関係が上下逆(例:強い正の相関が強い負の相関になる)になることが分かります。
倍で, 元の相関関係の位置関係が上下逆(例:強い正の相関が強い負の相関になる)になることが分かります。
【Case2】
両方のデータ![]() を
を![]() 倍したときの共分散
倍したときの共分散![]() は,
は,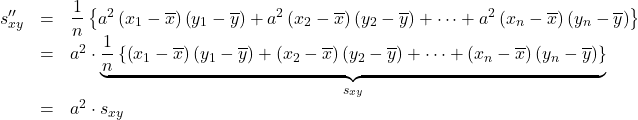
このように, 共分散は![]() 倍されます。
倍されます。
また, 標準偏差![]() はそれぞれ,
はそれぞれ, ![]() であるから, このときの相関係数
であるから, このときの相関係数![]() は,
は, 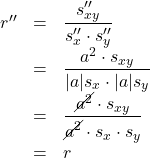
となり, 元の相関係数と変化がないことがわかる。
②分散は
③標準偏差は
④相関係数は片方
以下関連記事
 高校数学:データの値がa増えたらどうなる
高校数学:データの値がa増えたらどうなる  高校数学:データxをax+bにするとどうなるか
高校数学:データxをax+bにするとどうなるか 数樂管理人のブログ
数樂管理人のブログ 
