こんにちは。今回は群数列についてです。例題を解きながら見ていきましょう。
【例題】次のように正の奇数の数列を, 順に2個, 4個, 6個, ![]() の群に分ける。
の群に分ける。
1 , 3| 5, 7, 9, 11| 13, 15, 17, 19, 21, 23 | ![]()
(1) ![]() 群に入る最初の奇数を求めよ。
群に入る最初の奇数を求めよ。
(2) 8群に入るすべての数の和を求めなさい。
【解法】
(1) 群がないときの一般項を考えると, ![]()
このとき群に入る個数は2個, 4個, 6個, ![]() なので個数の数列は,
なので個数の数列は, ![]() である。
である。 ![]() のとき,
のとき, ![]() 群の最初の数は数列
群の最初の数は数列![]() の何番目かというと
の何番目かというと ![]() (個数)の
(個数)の![]() 番目までの和に1(
番目までの和に1(![]() 群の1番目)をたしたものであることがわかる。
群の1番目)をたしたものであることがわかる。
したがって, その何番目かというのを求めると, ![]() 番目として
番目として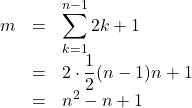
これは![]() のときも成り立つ。
のときも成り立つ。
これで何番目かわかったので,
求める数列は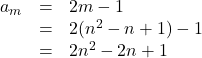
よって, ![]() (答)
(答)
(2) 8群の最初の数は, (1)より113, 8群は項数が![]() なので, 8群の末項は
なので, 8群の末項は![]()
したがって, 8群に入るすべての数の総和は, 等差数列の和の公式から, ![]()
![]() (答)
(答)
群数列n群の最初の数
![]() 群を無視して一般項
群を無視して一般項![]() を求める。
を求める。![]() 個数の数列
個数の数列![]() を求める。
を求める。![]()
![]() 番目までの個数の数列の和を求めそれに1を加える。これを
番目までの個数の数列の和を求めそれに1を加える。これを![]() とする。
とする。![]()
![]() の
の![]() を
を![]() で求めた
で求めた![]() で置き換える。
で置き換える。
 数樂管理人のブログ
数樂管理人のブログ 

