こんにちは。今回はデータで, データの値がそれぞれ![]() 増えた場合, 平均, 偏差, 分散, 標準偏差, 相関係数がどう変るか見ていきます。
増えた場合, 平均, 偏差, 分散, 標準偏差, 相関係数がどう変るか見ていきます。
平均
データ![]() の平均を
の平均を![]() とすると,
とすると, ![]()
ここで, データにそれぞれ![]() を加えて平均
を加えて平均![]() をとると,
をとると,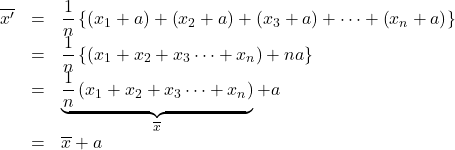
このように, 平均は![]() 増えることが分かります。
増えることが分かります。
偏差
偏差はデータと平均との差なので, データは![]() 増えて, 平均も先の計算から
増えて, 平均も先の計算から![]() 増えることが分かったので, 偏差に変化は起こりません。以下参照ください。
増えることが分かったので, 偏差に変化は起こりません。以下参照ください。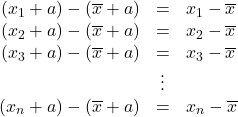
このように右辺の結果は, ![]() の値に左右されません。
の値に左右されません。
分散・標準偏差
偏差の2乗の平均が分散なので, 偏差に変化がないということは分散にも変化はありません。したがって, 分散を基にした標準偏差も変化はありません。
相関係数
2つのデータ![]() ,
, ![]() があるとき, 共分散
があるとき, 共分散![]() は次式で与えられます。
は次式で与えられます。![]()
また, それぞれのデータの標準偏差を![]() ,
, ![]() とすると,
とすると,
相関係数![]() は
は![]()
で与えられます。
今, データに![]() 加えたとしても, 上で示したように, それぞれの偏差には変化が起こりません。したがって分散, 標準偏差にも変化が起こらないので, 相関係数にも変化がないことが分かります。
加えたとしても, 上で示したように, それぞれの偏差には変化が起こりません。したがって分散, 標準偏差にも変化が起こらないので, 相関係数にも変化がないことが分かります。
データがa増えたら
①平均は 増える。
増える。
②偏差・分散・標準偏差・相関係数には変化はない。
データが 減った場合は①において, 平均は
減った場合は①において, 平均は 減ります。
減ります。
②偏差・分散・標準偏差・相関係数には変化はない。
データが
以下関連記事
 高校数学:データの値がa倍されたらどうなる
高校数学:データの値がa倍されたらどうなる  高校数学:データxをax+bにするとどうなるか
高校数学:データxをax+bにするとどうなるか 数樂管理人のブログ
数樂管理人のブログ 
