こんにちは。今回は帰納法と倍数の証明について書いておきます。
【例】![]() 自然数のとき,
自然数のとき,![]()
が13の倍数であることを証明せよ。
【解法】![]() のとき,
のとき, ![]()
で成り立つ。![]() のとき, 与式が13の倍数であると仮定すると,
のとき, 与式が13の倍数であると仮定すると, ![]() (
(![]() は自然数)
は自然数)![]()
![]() のとき,
のとき, 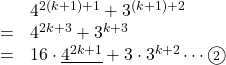
![]() の下線部は
の下線部は![]() より,
より, ![]() で置き換えることができるので,
で置き換えることができるので,
これを![]() に代入すると,
に代入すると, 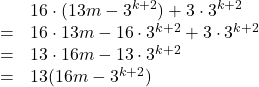
よって, ![]() のときも13の倍数になる事が示せた。
のときも13の倍数になる事が示せた。
したがって, すべての自然数において, ![]() は13の倍数である。
は13の倍数である。
【ここがコツ】 ![]() とおいたのを,
とおいたのを, ![]() に変形して
に変形して![]() の式に代入していくところ。また, それが代入できるように,
の式に代入していくところ。また, それが代入できるように, ![]() は
は![]() に変形, 代入した後,
に変形, 代入した後, ![]() の項が計算できるように,
の項が計算できるように, ![]() を
を![]() に変形するところがコツになります。
に変形するところがコツになります。
帰納法と倍数の証明
与式が何かの倍数であると仮定して式をつくり, それを変形して代入して解く。
今回のは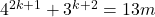 とおいたのを,
とおいたのを, 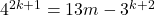 に変形して
に変形して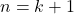 の式に代入。また, この変形した式が代入できるよう, 事前に累乗の指数部分を計算したり, 分解しておくこと。
の式に代入。また, この変形した式が代入できるよう, 事前に累乗の指数部分を計算したり, 分解しておくこと。
今回のは
 数樂管理人のブログ
数樂管理人のブログ 

