こんにちは。今回は数列に登場する和の公式を例題として証明していきます。
【例】自然数![]() に対して,
に対して, ![]()
が成り立つことを数学的帰納法を用いて証明せよ。
【解法】![]() のとき,
のとき, ![]() で成り立つ。
で成り立つ。![]() のとき, 与式の等式が成り立つとすると,
のとき, 与式の等式が成り立つとすると, ![]()
![]() のとき, 両辺に
のとき, 両辺に![]() を加えると,
を加えると, 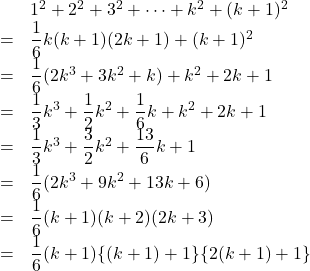
よって, ![]() のときも成り立つ。
のときも成り立つ。
したがって, すべての自然数に対して題意は成り立つ。
【結論が予測しやすい】![]() において, 与式の右辺が
において, 与式の右辺が![]() , つまり,
, つまり, ![]() なることは予測できます。したがって, そうなるように持ち込んでけばよい。今回は両辺に左辺の
なることは予測できます。したがって, そうなるように持ち込んでけばよい。今回は両辺に左辺の![]() 番目の項を加えることで解決しています。今回証明で因数分解を行っていますが, 因数定理とたすき掛けを用いて行っています。因数定理で適当な値が見つからなければ, 結果
番目の項を加えることで解決しています。今回証明で因数分解を行っていますが, 因数定理とたすき掛けを用いて行っています。因数定理で適当な値が見つからなければ, 結果![]() から予測してもいいでしょう。
から予測してもいいでしょう。
帰納法と等式の証明
結論として, 題意の等式の右辺の式において, 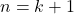 としたときの式を導ければよい。基本的には, 左辺の
としたときの式を導ければよい。基本的には, 左辺の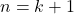 番目の項を両辺に加えて, 式変形していけばよい。
番目の項を両辺に加えて, 式変形していけばよい。
 数樂管理人のブログ
数樂管理人のブログ 

