こんにちは。今回は定数分離を用いた解法のご紹介です。例題を解きながら見ていきましょう。
【例】![]() についての3次方程式
についての3次方程式![]() の異なる実数解の個数を調べよ。
の異なる実数解の個数を調べよ。
【解法】与式の方程式における![]() を右辺に移項(定数分離)する。
を右辺に移項(定数分離)する。![]() とすると, これは関数
とすると, これは関数![]() と
と![]() のグラフの交点を求めていることに帰着する。
のグラフの交点を求めていることに帰着する。
したがって, ![]() のグラフを描いて,
のグラフを描いて, ![]() との交点の個数を調べることで, 異なる実数解の個数がわかるという仕組みになっている。 2つのグラフを描いてみると,
との交点の個数を調べることで, 異なる実数解の個数がわかるという仕組みになっている。 2つのグラフを描いてみると,
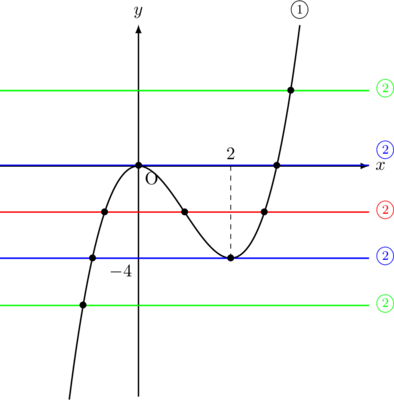
赤の線のとき, グラフの交点は3つあり, 異なる実数解は3個あることがわかり,
青の線のとき, グラフの交点は2つあり, 異なる実数解は2個あることがわかり,
緑の線のとき, グラフの交点は1つあり, 異なる実数解は1個あることがわかる。
したがって, 求める
【例】関数![]() に点
に点![]() から異なる接線が3本引けるような
から異なる接線が3本引けるような![]() の範囲を求めよ。
の範囲を求めよ。
【解法】接線なので, 関数を微分して接線を求める作業をします。接点の座標は, 関数上の点![]() とします。
とします。![]() より接線の方程式は,
より接線の方程式は, ![]()
よって, ![]() が接線の方程式となる。
が接線の方程式となる。
これが, ![]() を通るので,
を通るので, ![]()
となり, この![]() の3次方程式が異なる3つの実数解(接点が3つ)を持てばよいので,
の3次方程式が異なる3つの実数解(接点が3つ)を持てばよいので, ![]() ,
, ![]() のグラフを描いて
のグラフを描いて![]() の範囲を求めると,
の範囲を求めると, ![]()
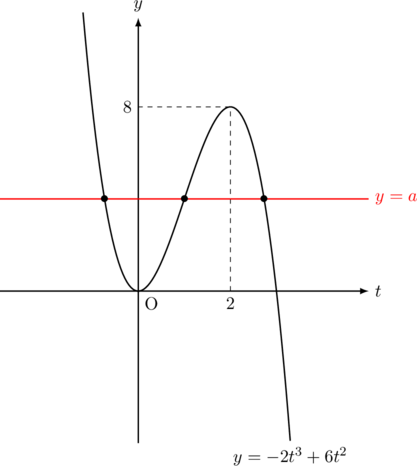
定数分離の基本解法
基本的には定数部と変数部(関数部)に分けて, 2つのグラフの交点の個数を調べる。
比較的頻出の技なので, 使いこなせた方がよい。
 数樂管理人のブログ
数樂管理人のブログ 

