こんにちは。定数分離の考え方を用いた解法の紹介です。例題を見ながらいきましょう。この類の問題を以下のような形で直接解くことはあまりないかもしれませんが, 解法の勉強として提示しておきます。
定数を含む式か含まない式かで分離
【例】 についての2次方程式
についての2次方程式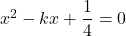 の
の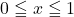 の範囲における異なる実数解の個数を調べよ。
の範囲における異なる実数解の個数を調べよ。
【解法】基本的な考え方は定数分離と同じなんですが, 今回は定数ではなく, 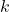 を含む式と
を含む式と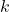 を含まない式で分離します。すなわち,
を含まない式で分離します。すなわち,
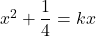 として,
として,
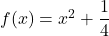 ,
, 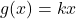 の2つのグラフの交点の個数を調べることにします。
の2つのグラフの交点の個数を調べることにします。
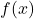 と
と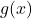 が接するとき, 方程式
が接するとき, 方程式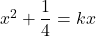 は重解を持つので,
は重解を持つので,
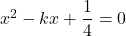 として, 判別式
として, 判別式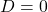 を求める。
を求める。
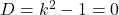 から,
から, 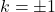 となるが,
となるが, 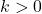 より,
より, 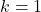 のとき, 解は1つ(
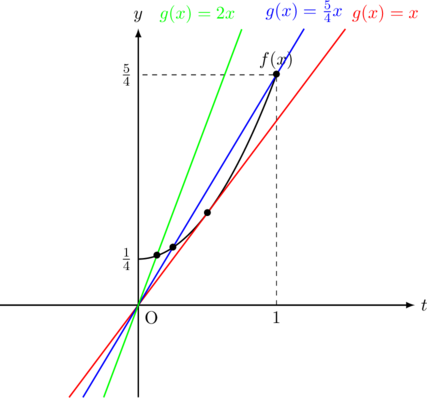
のとき, 解は1つ(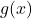 は赤のグラフ)になる。この
は赤のグラフ)になる。この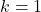 の傾きより小さいと2つのグラフの交点は存在しないので, 解の個数は0個になる。また, この赤のグラフ(傾き1)より傾きが大きくなると, 2つのグラフの交点は2つになり, 交点を2つもったまま, その傾きが最大になるのが点
の傾きより小さいと2つのグラフの交点は存在しないので, 解の個数は0個になる。また, この赤のグラフ(傾き1)より傾きが大きくなると, 2つのグラフの交点は2つになり, 交点を2つもったまま, その傾きが最大になるのが点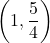 を通るとき, 解はちょうど2つになるので, この座標を
を通るとき, 解はちょうど2つになるので, この座標を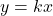 に代入すると,
に代入すると, 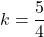 (
(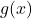 は青のグラフ)。したがって,
は青のグラフ)。したがって, 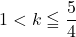 (赤より大きく青以下の間の範囲)のとき解は2つになる。この
(赤より大きく青以下の間の範囲)のとき解は2つになる。この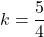 の傾きより大きいと2つのグラフは交点を1つしか持たない(例 :
の傾きより大きいと2つのグラフは交点を1つしか持たない(例 : 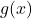 は緑のグラフ)ので, 解の個数も1つとなる。
は緑のグラフ)ので, 解の個数も1つとなる。
以上より,
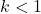 のとき, 解は0個
のとき, 解は0個
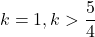 のとき, 解は1個
のとき, 解は1個
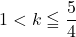 のとき, 解は2つ
のとき, 解は2つ
定数分離の応用
定数を含む式と定数を含まない式で分離して, 交点の個数を調べる。
![]() についての2次方程式
についての2次方程式![]() の
の![]() の範囲における異なる実数解の個数を調べよ。
の範囲における異なる実数解の個数を調べよ。![]() を含む式と
を含む式と![]() を含まない式で分離します。すなわち,
を含まない式で分離します。すなわち, ![]() として,
として, ![]() ,
, ![]() の2つのグラフの交点の個数を調べることにします。
の2つのグラフの交点の個数を調べることにします。
 数樂管理人のブログ
数樂管理人のブログ 

