3次関数の接線と接点の関係について書いておきます。
3次関数![]() の
の![]() における接線
における接線![]() は接点
は接点![]() と接点以外の共有点
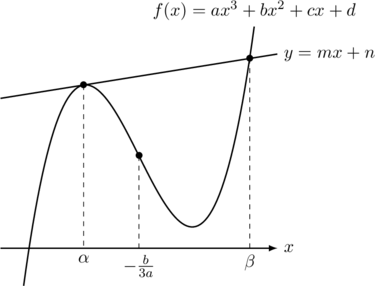
と接点以外の共有点![]() を持つわけで, 2つのグラフの概形を描くと次のようになります。グラフ中の
を持つわけで, 2つのグラフの概形を描くと次のようになります。グラフ中の![]() は変曲点の
は変曲点の![]() 座標です。
座標です。
念のため変曲点の![]() 座標の求めておくと,
座標の求めておくと, ![]()
![]()
![]() として,
として, ![]() を得る。
を得る。
このとき,
となるが, この左辺の式は, 接線と
ここで,
となる。これで接点の
また,
と変形でき, これの意味するところは,
これは, グラフの対称性や性質などから, 次のように表せる。
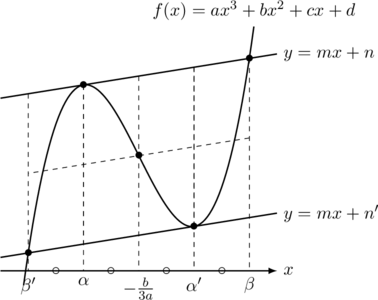
このように8個の合同な平行四辺形ができる。このような関係を知っておくと面積を求めるときの接点の座標の関係など便利なことが多い。
3次関数の接線と接点
3次関数![]() のグラフ上の点
のグラフ上の点![]() における接線が,
における接線が, ![]() のグラフと再び交わる点を
のグラフと再び交わる点を![]() とすると,
とすると,![]()
の関係が成り立つ。
これは, 接点![]() から変曲点
から変曲点![]() までの水平方向の距離と変曲点
までの水平方向の距離と変曲点![]() から接線の交点
から接線の交点![]() までの水平距離の比が
までの水平距離の比が![]() であることを意味している。
であることを意味している。
 数樂管理人のブログ
数樂管理人のブログ 

