こんにちは。高校数学の定期テストでよく見かける二次関数の符号決定などの解法を書いておきます。例題を解きながら見ていきましょう。
【例】二次関数![]() のグラフが次のように表されるとき,
のグラフが次のように表されるとき, ![]() の符号を求めなさい。
の符号を求めなさい。
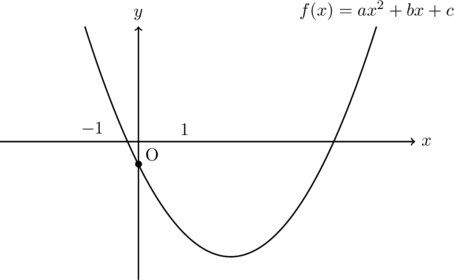
【解法】
軸は
この軸の符号はグラフから正
以上このようにして求めます。
軸を求めるとき, 平方完成が面倒なら軸の式
符号決定
グラフの概形をしっかり読み取って, 符号を決定しよう。![]() はグラフが上に凸か下に凸かで符号が決まる。
はグラフが上に凸か下に凸かで符号が決まる。![]() はグラフと
はグラフと![]() 軸との交点の符号で決まる。
軸との交点の符号で決まる。![]() の符号は軸で決めることが多いので, 軸の式
の符号は軸で決めることが多いので, 軸の式![]() をしっかり覚えておこう。
をしっかり覚えておこう。
 数樂管理人のブログ
数樂管理人のブログ 

