こんにちは。今回は変量![]() のデータが
のデータが![]() ,
, ![]() に変換された場合どう変化するか見ていきましょう。
に変換された場合どう変化するか見ていきましょう。
平均
データ ![]() の平均を
の平均を![]() とすると,
とすると,![]()
ここで, データをそれぞれ![]() 倍して
倍して![]() 加えた平均
加えた平均![]() をとると,
をとると, 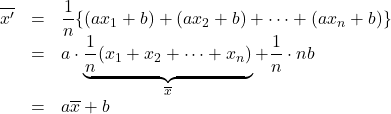
同様に, データ ![]() の平均を
の平均を![]() とすると,
とすると,
このデータをそれぞれ![]() 倍して
倍して![]() 加えた平均
加えた平均![]() は,
は, ![]()
となる。
このようにデータ![]() の平均は
の平均は![]() 倍され
倍され![]() 増え, データ
増え, データ![]() の平均は
の平均は![]() 倍され
倍され![]() 増えます。
増えます。
偏差
偏差はそれぞれのデータから平均を引いたものなので,
データ![]() の偏差は,
の偏差は, 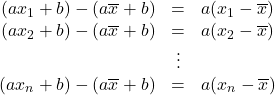
データ![]() の偏差も同様に,
の偏差も同様に,
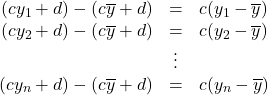
このように偏差は![]() 倍,
倍, ![]() 倍されます。
倍されます。
分散
分散は偏差の2乗の平均ですから, データ![]() の元の分散を
の元の分散を![]() とすると,
とすると, ![]()
![]() 倍して
倍して![]() 加えたデータでは, 偏差が
加えたデータでは, 偏差が![]() 倍されるので, その分散
倍されるので, その分散![]() は,
は, ![Rendered by QuickLaTeX.com \begin{array}{rcl}s'_x^2&=&\dfrac{1}{n}\left[\left\{a\left(x_1-\overline{x}\right)\right\}^2+\left\{a\left(x_2-\overline{x}\right)\right\}^2+\left\{a\left(x_3-\overline{x}\right)\right\}^2+\cdots+\left\{a\left(x_n-\overline{x}\right)\right\}^2\right]\\&=&a^2\cdot \underbrace{ \dfrac{1}{n}\left\{\left(x_1-\overline{x}\right)^2+\left(x_2-\overline{x}\right)^2+\left(x_3-\overline{x}\right)^2+\cdots+\left(x_n-\overline{x}\right)^2\right\} }_{\LARGE{s_x^2}} \\&=&a^2\cdot s_x^2\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-02e0ab8882683d6c4fc309d465247e5a_l3.png)
同様に, ![]() 倍して
倍して![]() 加えたデータでは, 偏差が
加えたデータでは, 偏差が![]() 倍されるので, その分散
倍されるので, その分散![]() は,
は, ![]()
したがって, 分散は元の分散の![]() 倍,
倍, ![]() 倍になる。
倍になる。
標準偏差
標準偏差は分散の正の平方根なので,
分散が![]() 倍,
倍, ![]() 倍されるなら標準偏差は
倍されるなら標準偏差は![]() 倍,
倍, ![]() 倍されます。絶対値が付いてるのは
倍されます。絶対値が付いてるのは![]() ,
, ![]() の場合を考慮してのことです。
の場合を考慮してのことです。
つまり, ![]() ,
, ![]() になります。
になります。
相関係数
2つのデータ![]() ,
, ![]() があるとき, 共分散
があるとき, 共分散![]() は次式で与えられます。
は次式で与えられます。![]()
また, それぞれのデータの標準偏差を![]() ,
, ![]() とすると,
とすると,
相関係数![]() は
は![]()
で与えられます。
データ![]() の偏差はそれぞれ
の偏差はそれぞれ![]() 倍,
倍, ![]() 倍されているので, 共分散
倍されているので, 共分散![]() は,
は,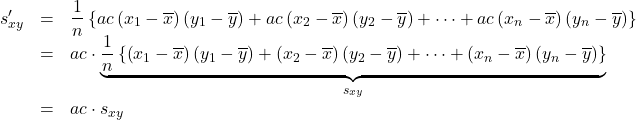
このように, 共分散は![]() 倍されます。
倍されます。
また, 標準偏差![]() はそれぞれ,
はそれぞれ, ![]() であるから, このときの相関係数
であるから, このときの相関係数![]() は,
は, 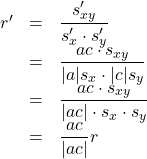
となり, ![]() なら, 元の相関係数と変化がなく,
なら, 元の相関係数と変化がなく, ![]() なら相関係数の符号が反対になる (例:強い正の相関が強い負の相関になる) ことがわかる。
なら相関係数の符号が反対になる (例:強い正の相関が強い負の相関になる) ことがわかる。
ちなみに, ![]() のデータだけ
のデータだけ![]() に変換した場合の相関係数
に変換した場合の相関係数![]() は,
は, ![]()
となり, ![]() なら元の相関係数と変わらず,
なら元の相関係数と変わらず, ![]() なら相関係数の符号が反対になる。
なら相関係数の符号が反対になる。
データがa倍されb加えると
①平均は 倍され
倍され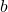 増える。
増える。
②偏差は 倍される。
倍される。
③分散は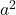 倍になる。
倍になる。
④標準偏差は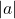 倍になる。
倍になる。
⑤相関係数は片方のデータをすべて 倍して
倍して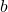 加えたときは
加えたときは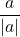 倍される。
倍される。
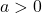 なら相関係数に変化なし,
なら相関係数に変化なし, 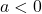 なら相関係数の符号が反対になる。
なら相関係数の符号が反対になる。
もう一方のデータをすべて 倍して
倍して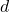 加えたなら,
加えたなら, 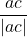 倍される。
倍される。
 なら相関係数に変化なし,
なら相関係数に変化なし,  なら相関係数の符号が反対になる。
なら相関係数の符号が反対になる。
②偏差は
③分散は
④標準偏差は
⑤相関係数は片方のデータをすべて
もう一方のデータをすべて
以下関連記事
 高校数学:データの値がa倍されたらどうなる
高校数学:データの値がa倍されたらどうなる  高校数学:データの値がa増えたらどうなる
高校数学:データの値がa増えたらどうなる 数樂管理人のブログ
数樂管理人のブログ 

